El concepto de campo

Un fluido en reposo puede conceptualizarse como un sistema termodinámico, es decir, un sistema sujeto a las leyes de la termodinámica clásica. Esta teoría describe únicamente estados de equilibrio que, por definición, son independientes del tiempo. La descripción de un fluido en movimiento, que es el objeto fundamental de la mecánica de fluidos, trasciende a la termodinámica clásica, ya que involucra el estudio de la evolución del medio en el espacio y en el tiempo. En otras palabras, nos interesa estudiar cómo cambian espacial y temporalmente las variables de campo que describen al fluido.

Un campo es cualquier cantidad física que a cada instante toma diferentes valores en distintos puntos del espacio. Los campos son las cantidades físicas básicas en el enfoque del continuo. Matemáticamente, los campos son funciones continuas del espacio y del tiempo. Podemos distinguir entre campos escalares, como la temperatura, $T(x,y,z,t)$, y campos vectoriales como la velocidad del fluido, $\mathit{u}(x,y,z,t)$ (ver Fig. 4 y Fig. 5).

También podemos denotarlos en la forma $T(\mathit{r},t)$ y $\mathit{u}(\mathit{r},t)$, donde $\mathit{r}=(x,y,z)$ es el vector de posición.

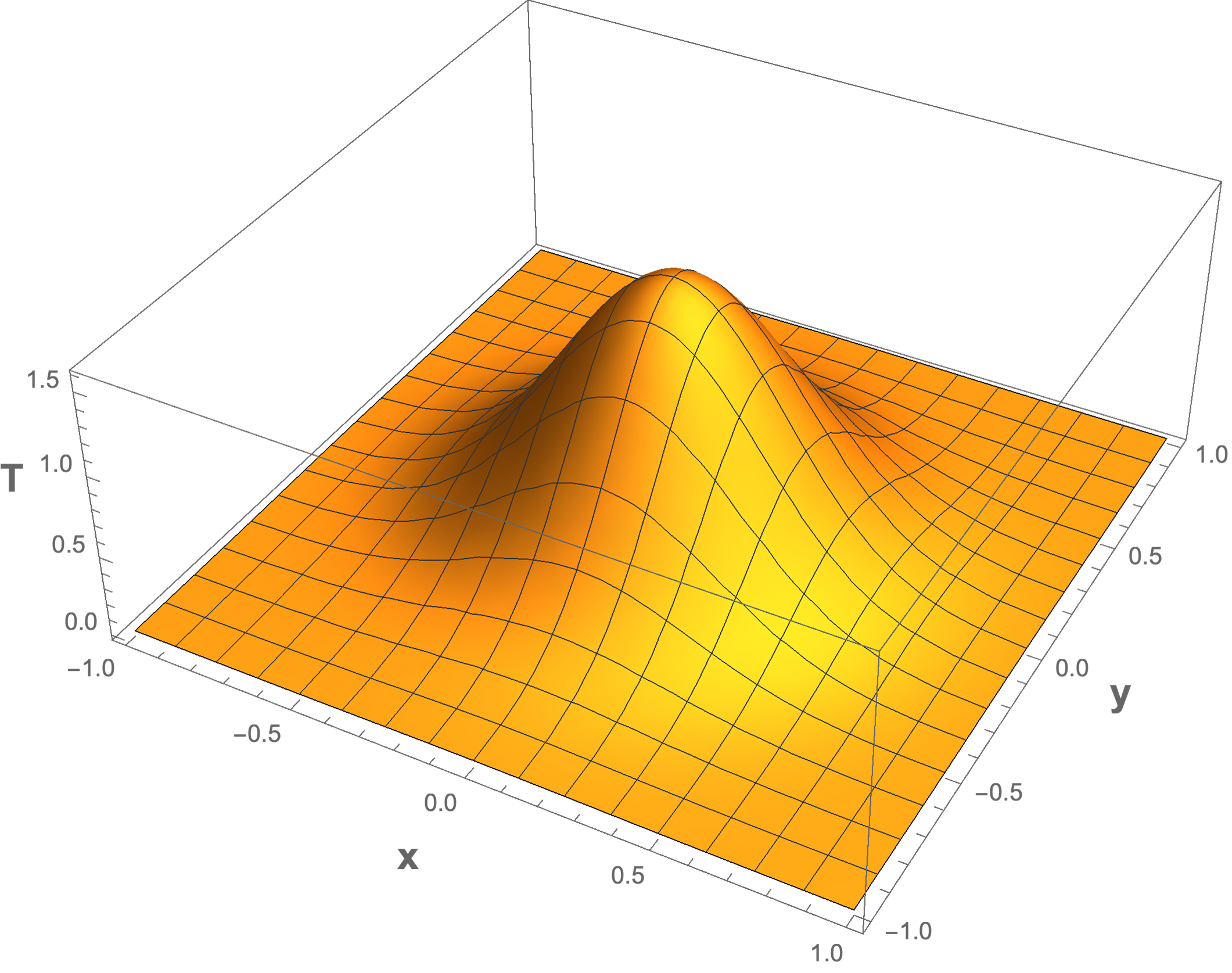
Fig. 4 Campo escalar de temperatura en dos dimensiones de una fuente de calor localizada en el origen.

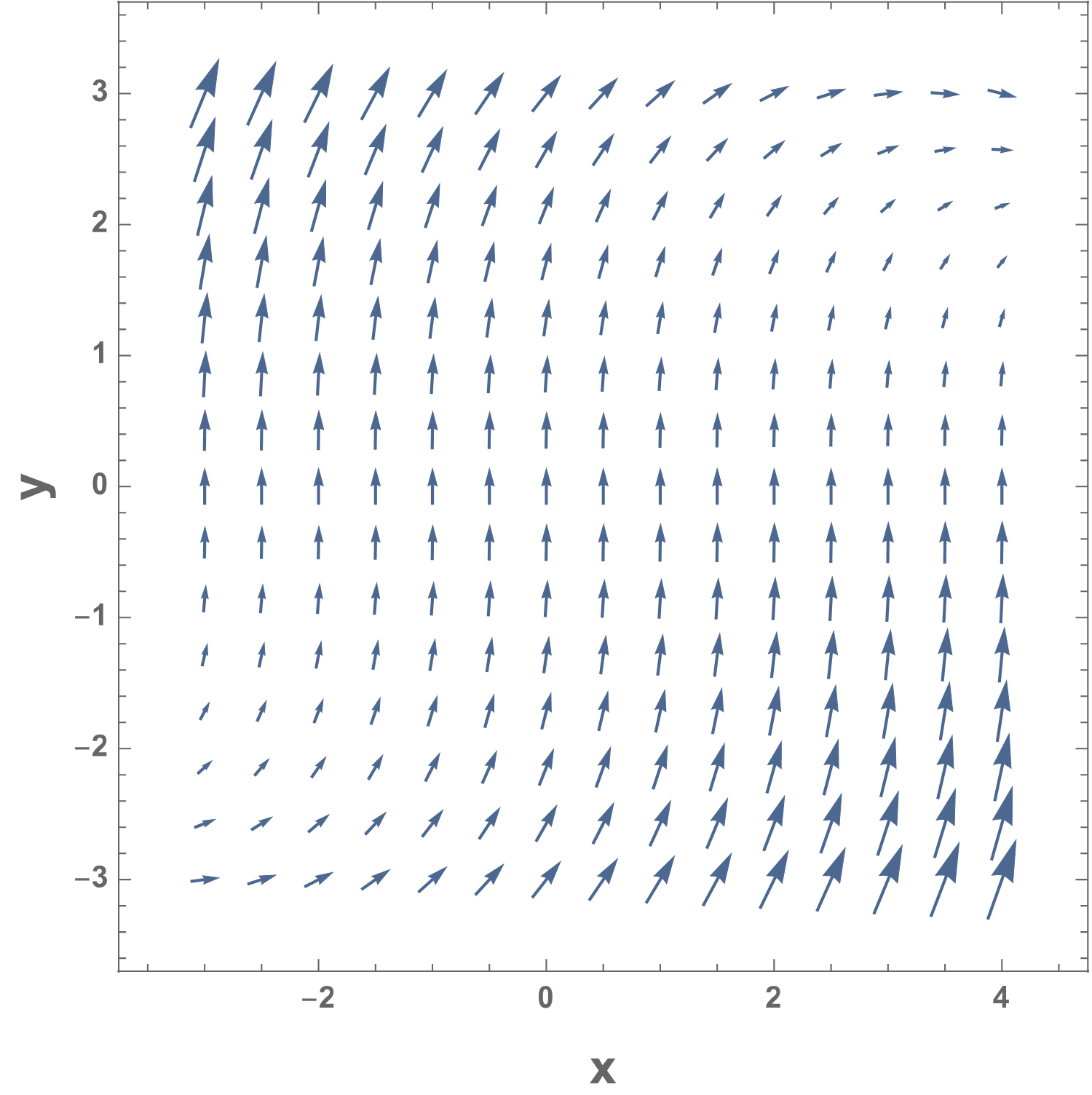
Fig. 5 Campo vectorial de velocidades bidimensional.

Mientras que un campo escalar se puede determinar por un único valor a cada instante de tiempo y en cada punto del espacio, un vector en un espacio tridimensional requiere de tres componentes para su determinación completa. Lo que caracteriza matemáticamente a un escalar o a un vector son sus propiedades de transformación ante rotaciones de los ejes coordenados. Los escalares son cantidades invariantes ante rotaciones de coordenadas, mientras que los vectores satisfacen ciertas reglas precisas de transformación [5].

Un fluido en movimiento transporta diferentes cantidades físicas, por ejemplo, la masa, la cantidad de movimiento y la energía. Estos fenómenos de transporte están regidos por los principios fundamentales de la física denominados leyes de conservación, a saber, la ley de conservación de la masa, la segunda ley del movimiento de Newton y la ley de conservación de la energía. Al establecer estos principios en un medio continuo deformable, es decir, en un fluido, obtenemos las ecuaciones de conservación en términos de las variables de campo asociadas a dicho medio, por ejemplo, la densidad de masa, $\rho (x,y,z,t)$, el campo de velocidades $\mathit{u}(x,y,z,t)$, el campo de presiones, $p(x,y,z,t)$, y el campo de temperatura $T(x,y,z,t)$. Dichas ecuaciones determinan la evolución de las variables de campo y al resolverlas obtenemos su comportamiento espacio-temporal. En síntesis, podemos afirmar que resolver un problema en mecánica de fluidos significa determinar los campos físicos relevantes como funciones de las coordenadas espaciales y del tiempo. Resolver las ecuaciones de conservación para encontrar dichos campos no es el único método para obtenerlos. Mediante la experimentación es posible determinarlos, aunque evidentemente esto requiere de sistemas de medición específicos y puede estar constreñido por limitaciones tecnológicas o prácticas.

Previamente a la obtención de las ecuaciones de conservación, es conveniente establecer ciertas ideas básicas acerca de la descripción del movimiento de los fluidos sin considerar las fuerzas que lo originan, lo que se conoce como la cinemática de flujo.