La ecuación de balance de momento lineal

La ecuación de balance de la cantidad de movimiento o momento lineal no es otra cosa más que la expresión de la segunda ley de Newton aplicada a un fluido. Esta ley nos dice que la variación en el tiempo del momento de un cierto cuerpo es igual a la fuerza total que actúa sobre él. Si consideramos un cuerpo de masa \(m\) que se desplaza con velocidad \({\bf v}\), el momento lineal asociado es \({\bf p}=m{\bf v}\). En términos de \({\bf p}\), la segunda ley de Newton toma la forma

\[\frac{d{\bf p}}{dt} = {\bf F}\]

donde \({\bf F}\) es la fuerza total que actúa sobre el cuerpo, es decir, la suma de todas las fuerzas presentes. Si en alguna situación particular la fuerza total es nula, \({\bf F}=0\), tenemos entonces que

\[\frac{d{\bf p}}{dt} = 0,\]

de manera que el momento \({\bf p}\) se mantiene constante, es decir, se conserva. Por otra parte, si la situación es tal que \({\bf F}\neq 0\), el momento no se conserva. Ya que esta es la situación más general, resulta conveniente hablar de la ecuación de balance de momento, en vez de la ecuación de conservación de momento. Hay que notar, sin embargo, que en muchos libros se utiliza esta última denominación.

Para obtener la ecuación mencionada, partiremos de la forma más común de la segunda ley de Newton que para una partícula de masa \(m\) se expresa como

\[m {\bf a} = {\bf F},\]

donde \({\bf a}\) es la aceleración de la partícula causada por la fuerza total \({\bf F}\) que actúa sobre la misma. Cuando tratamos con un fluido, debemos utilizar cantidades definidas por unidad de volumen ya que estamos tratando con un medio continuo que se extiende en el espacio. Si consideramos un volumen de control unitario, la segunda ley de Newton para un fluido se puede escribir como

(46)\[\rho {\bf a} = {\bf f},\]

donde \(\rho\) es la densidad de masa del fluido, \({\bf a}\) es la aceleración del elemento de volumen y \({\bf f}\) la fuerza total por unidad de volumen cuyas unidades son \(\left[ N/m^3 \right]\).

Recordando que la aceleración en un fluido se expresa como

\[{\bf a} = \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u},\]

donde \({\boldsymbol u}\) es el campo de velocidades, y sustituyendo en la ecuación (46), obtenemos

(47)\[\rho \left( \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u} \right) = {\bf f}\]

donde debemos especificar la forma explícita de \({\bf f}\).

Fuerzas de cuerpo y fuerzas de superficie

En general, podemos distinguir entre dos tipos de fuerzas que actúan sobre un fluido, las fuerzas de cuerpo o volumen que denotaremos por \({\bf f}_c\), y las fuerzas de superficie, denotadas por \({\bf f}_s\). Las fuerzas de cuerpo o volumen son de largo alcance, es decir, no se requiere tener contacto para transmitir la fuerza. Además, actúan sobre el volumen del cuerpo como un todo, independientemente de la forma del cuerpo. Por tanto, no dependen de la superficie del cuerpo. Ejemplos típicos de estas fuerzas son la gravedad y las fuerzas electromagnéticas. La fuerza de Coriolis que aparece en fluidos en rotación (como la atmósfera o el oceáno) también es una fuerza de cuerpo.

Para los problemas que estudiaremos en este curso, la gravedad es la fuerza de cuerpo relevante. Sabemos que para una partícula dicha fuerza tiene la forma

\[{\bf F}_g =m {\bf g},\]

donde \({\bf g}\) es la aceleración de la gravedad. En un fluido, podemos expresar dicha fuerza por unidad de volumen como

(48)\[{\bf f}_g =\rho {\bf g}.\]

Por otra parte, las fuerzas de superficie son de corto alcance. Son fuerzas de contacto y su origen es molecular, es decir, dependen de la estructura molecular de la materia. Actúan sobre cada elemento de área o superficie, por lo que son dependientes de la forma del cuerpo. Ejemplos de estas fuerzas son la fuerza de presión y la fuerza de fricción que denotaremos por \({\bf f}_p\) y \({\bf f}_{visc}\), respectivamente. Como veremos, la fuerza de fricción tiene su origen en una propiedad intrínseca de cada fluido llamada viscosidad.

En general, las fuerzas de superficie son más complicadas de describir matemáticamente que las fuerzas de cuerpo. Por ejemplo, si querermos describir la manera en que actúa la gravedad sobre un cuerpo de forma irregular que cae libremente en la atmósfera, podemos suponer sin problema que la gravedad actúa a través de un único punto conocido como el centro de masa del cuerpo. Así, la gravedad queda completamente determinada a partir de un vector. Sin embargo, si deseamos describir cómo actúan las fuerzas de presión y fricción ejercidas por el aire sobre el mismo cuerpo necesitamos conocer la forma precisa de su superficie, ya que en cada punto dichas fuerzas actuarán de manera diferente, lo que acarrea una complicación matemática adicional.

Las fuerzas de presión y fricción se originan a partir de los esfuerzos mecánicos que ejerce el fluido. Recordemos que un esfuerzo es una fuerza ejercida sobre una superficie determinada y pueden ser normales o cortantes. Los esfuerzos normales actúan de manera normal o perpendicular a la superficie, mientras que los esfuerzos cortantes actúan tangencialmente a la misma. De la experiencia cotidiana sabemos que ante la aplicación de esfuerzos cortantes, por ejemplo, cuando se arrastra una cuchara en un fluido o se intenta deslizar una placa sólida sobre la superficie del mismo, fluidos como la glicerina o el lodo tienen un comportamiento físico distinto del agua y del aire, por tanto, se caracterizan matemáticamente de manera diferente. En otras palabras, cuando se aplica un esfuerzo a un fluido, este responderá deformándose de una manera característica. Es precisamente la relación entre esfuerzos y deformaciones lo que determina el tipo de fluido en cuestión.

En este curso, nos enfocaremos exclusivamente a un grupo de fluidos conocidos como \(\textit{ Newtonianos}\) que son los más simples y afortunadamente los más comunes en la Tierra puesto que el agua y el aire pertencen a este grupo. Existen toda una variedad de fluidos denominados de manera genérica como fluidos reológicos o no Newtonianos que presentan un comportamiento más complejo.

Para la descripción de las fuerzas de superficie es necesario introducir una cantidad conocida como el tensor de esfuerzos mecánicos que denotaremos por \(\tilde{{\boldsymbol \sigma}}\). En un espacio tridimensional un vector es una cantidad que tiene tres componentes y cumple con ciertas propiedades de transformación ante rotaciones de ejes coordenados. Por su parte, la cantidad \(\tilde{{\boldsymbol \sigma}}\) es un tensor que cuenta con nueve componentes y cumple también con ciertas propiedades de transformación. Matemáticamente, \(\tilde{{\boldsymbol \sigma}}\) se puede visualizar como una matriz de \(3 \times 3\), es decir,

(49)\[ \begin{align}\begin{aligned}\notag\\\begin{split} \tilde{{\boldsymbol \sigma}} = \left[ \begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yx}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{matrix} \right]\end{split}\end{aligned}\end{align} \]

Los elementos que se encuentran en la diagonal son los esfuerzos normales, mientras que los que están fuera de ella son esfuerzos tangenciales. Una manera de visualizar gráficamente los esfuerzos en un fluido es mediante un volumen de control cúbico como el mostrado en la figura Fig. 32. Notemos que en cada cara del cubo existen dos esfuerzos tangenciales o cortantes y un esfuerzo normal. El primer índice en los elementos del tensor de esfuerzos se refiere a la cara en donde está siendo aplicado, mientras que el segundo índice se refiere a la dirección en que se aplica. Por ejemplo, el esfuerzo cortante \(\sigma_{yx}\) corresponde a la cara \(y\), es decir, la cara cuya normal apunta en la dirección \(y\), y está siendo aplicado en la dirección \(x\). Por su parte, el esfuerzo normal \(\sigma_{yy}\) corresponde a la cara \(y\) y está aplicado en la dirección \(y\).

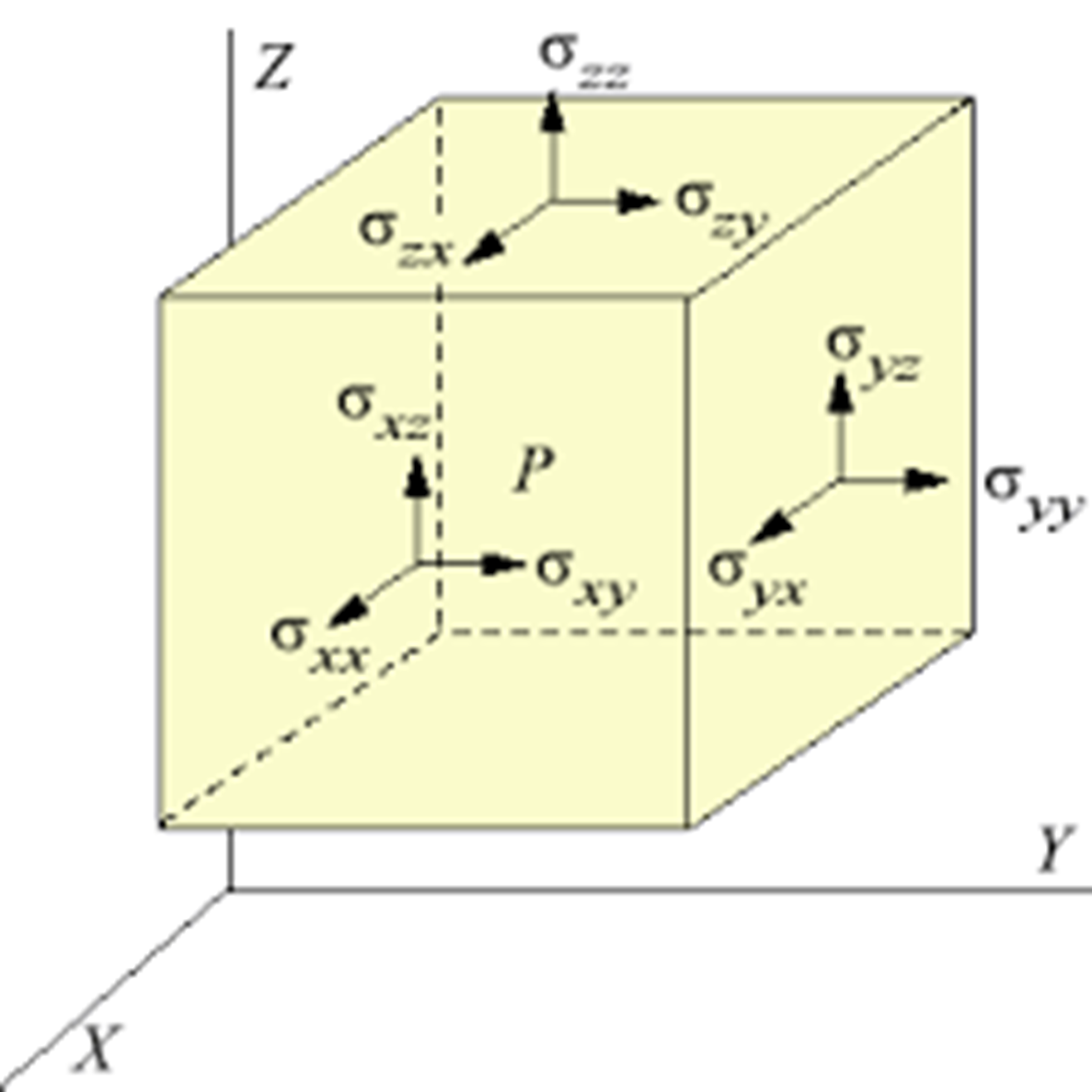
Fig. 32 Componentes del tensor de esfuerzos en las caras de un volumen de control cúbico.

Veamos cómo podemos determinar la forma explícita de la fuerza de presión. Para esto consideremos un volumen de control fijo en el espacio, como el paralelepípedo mostrado en la figura Fig. 39, cuyos lados son \(\Delta x\), \(\Delta y\) y \(\Delta z\). Nos preguntamos ahora cuál es la fuerza neta que ejerce la presión sobre las caras del cubo. La presión es un esfuerzo normal de modo que actúa de manera perpendicular a una superficie dada. Ya que es la misma en todas direcciones, la existencia de una fuerza neta por unidad de volumen se debe a que la presión varía de un punto a otro. Así, la fuerza ejercida sobre la cara izquierda del cubo es el producto de la presión por el área de la cara correspondiente, es decir,

\[p \;\Delta y \Delta z \; \hat{{\bf i}} \]

donde \(p(x,y,z,t)\) es la función escalar que denominamos presión y el vector unitario \(\hat{{\bf i}}\) indica que la fuerza apunta hacia la derecha. A su vez, en la cara opuesta donde la presión es ligeramente diferente la fuerza es

\[-\left( p + \frac{\partial p}{\partial x} \Delta x \right) \;\Delta y \Delta z \; \hat{{\bf i}}, \]

apuntando en dirección negativa. Sumando estas dos contribuciones obtenemos la fuerza resultante en dirección \(x\), es decir,

\[- \frac{\partial p}{\partial x} \; \Delta x \;\Delta y \; \Delta z \; \hat{{\bf i}}, \]

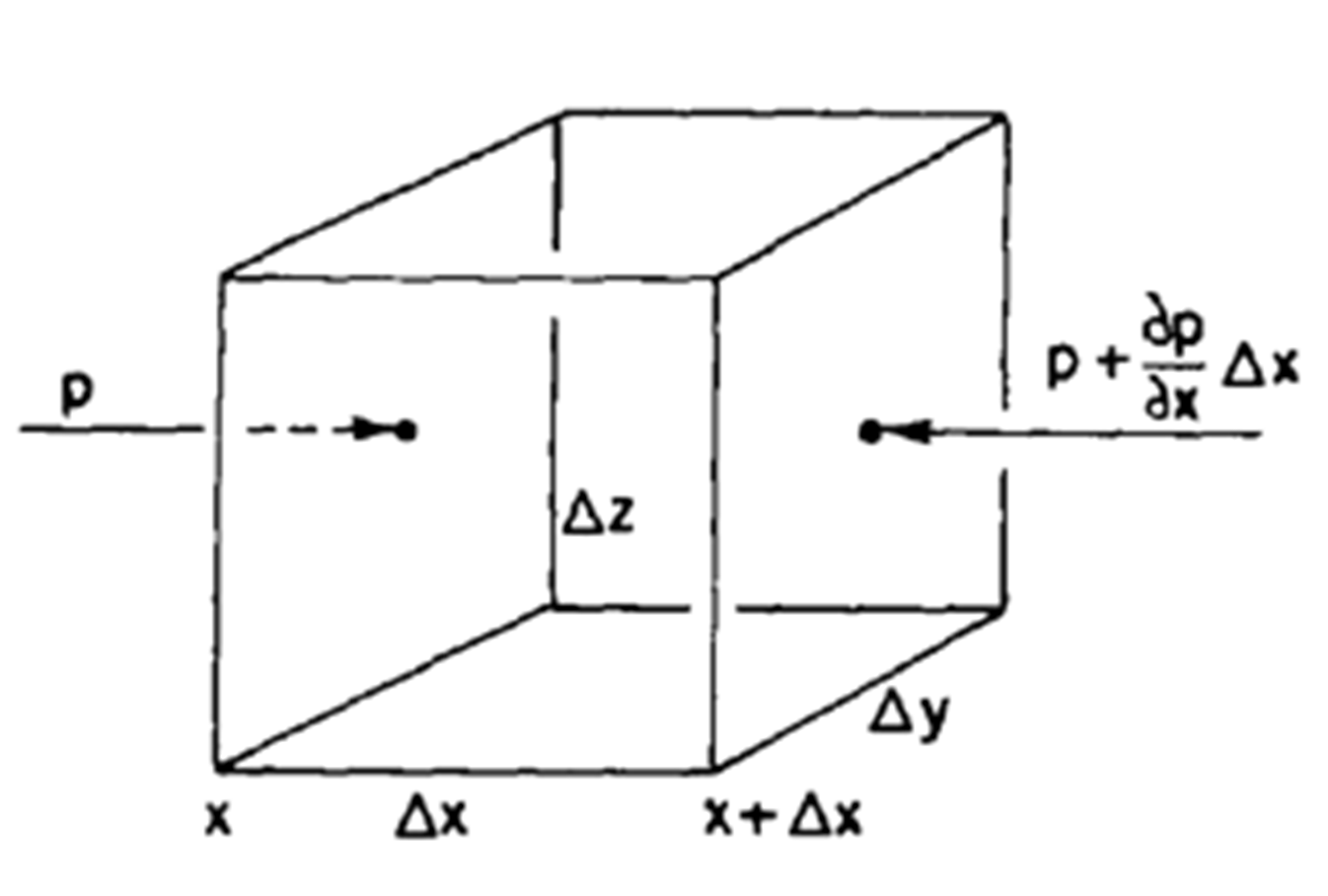
Fig. 33 Presión ejercida por un fluido en las caras de un volumen de control cúbico.

Haciendo un análisis similar en los dos pares de caras restantes, encontramos que las fuerzas resultantes en las direcciones \(y\) y \(z\) son, respectivamente,

\[- \frac{\partial p}{\partial y} \; \Delta x \;\Delta y \; \Delta z \; \hat{{\bf j}}, \]

\[- \frac{\partial p}{\partial z} \; \Delta x \;\Delta y \; \Delta z \; \hat{{\bf k}}. \]

Sumando las contribuciones en las tres direcciones, la fuerza de presión total sobre el cubo es

\[{\bf F}_p = \left( - \frac{\partial p}{\partial x} \; \hat{{\bf i}} - \frac{\partial p}{\partial y} \hat{{\bf j}} \frac{\partial p}{\partial z} \hat{{\bf k}} \right) \; \Delta x \;\Delta y \; \Delta z.\]

Si denotamos al volumen del cubo como \(\Delta V =\Delta x \;\Delta y \; \Delta z\), la fuerza de presión por unidad de volumen es:

\[{\bf f}_p = \lim_{\Delta V \rightarrow 0} \; \frac{{\bf F}_p}{\Delta V} = \left( - \frac{\partial p}{\partial x} \; \hat{{\bf i}} - \frac{\partial p}{\partial y} \hat{{\bf j}} - \frac{\partial p}{\partial z} \hat{{\bf k}} \right), \]

donde se ha tomado el límite cuando el volumen de control tiende a cero, por lo que en cada punto del fluido la fuerza de presión es

(50)\[{\bf f}_p = -{\boldsymbol \nabla} p.\]

Regresando a la ecuación de balance de momento (47) y sustituyendo explícitamente las fuerzas de cuerpo (gravedad) y presión (ecuaciones (48) y (50), respectivamente), obtenemos:

(51)\[\rho \left( \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u} \right) = -{\boldsymbol \nabla} p + \rho {\bf g} + {\bf f}_{visc},\]

donde falta especificar la forma explícita de la fuerza de fricción.

La ecuación de Euler: el fluido ideal

Una primera aproximación al estudio del movimiento de los fluidos es suponer que las fuerzas de fricción son despreciables lo que indicaría que la viscosidad del fluido es despreciable o nula. Si la viscosidad es nula, el fluido no pude mojar las paredes con las que está en contacto, es decir, no se adhiere a las superficies sólidas, sino que se desliza sobre ellas. Un fluido con tales características se denomina fluido ideal. Las ecuaciones que gobiernan el movimiento de un fluido ideal compresible son

(52)\[ \frac{\partial \rho}{\partial t} + {\boldsymbol \nabla} \cdot (\rho {\boldsymbol u}) =0,\]

(53)\[\rho \left[ \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u} \right] = -{\boldsymbol \nabla} p + \rho {\bf g},\]

donde podemos identificar a la ecuación de conservación de la masa (52), mientras que la ecuación (53) se conoce como la ecuación de Euler, que es la expresión de la segunda ley de Newton para un fluido ideal. Notemos que las ecuaciones (52) y (53) forman un sistema de cuatro ecuaciones (una ecuación para la conservación de la masa y tres ecuaciones para el balance de momento) y cinco variables, es decir, la densidad, \(\rho\), la presión, \(p\) y las tres componentes del campo de velocidades \({\boldsymbol u} =(u,v,w)\). Por tanto, el sistema no está cerrado a menos que se dé una ecuación adicional. La ecuación faltante es la ecuación de estado para el fluido,

(54)\[\rho = \rho (T,P),\]

que indica la variación de la densidad como función de la temperatura y la presión. Por ejemplo, si el fluido es un gas ideal,la ecuación de estado es

(55)\[\rho = \frac{p}{RT}.\]

Debe enfatizarse que, un fluido ideal y un gas ideal son conceptos diferentes. A pesar de las simplificaciones, las ecuaciones (52), (53) y (55) permiten describir con una muy buena aproximación diversos problemas de interés, como la transmisión de ondas de sonido en el aire.

Por otra parte, si consideramos un fluido ideal incompresible cuya densidad es constante (\(\rho={\rm const.})\), el sistema de ecuaciones se reduce a

(56)\[ {\boldsymbol \nabla} \cdot {\boldsymbol u} =0,\]

(57)\[\rho \left[ \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u} \right] = -{\boldsymbol \nabla} p + \rho {\bf g},\]

donde tenemos cuatro ecuaciones para cuatro incógnitas, es decir, la presión, \(p\), y las tres componentes del campo de velocidades \({\boldsymbol u} =(u,v,w)\). Estas ecuaciones permiten, en particular, describir de manera precisa la propagación de ondas superficiales en agua. Veremos también que pueden aplicarse a muchas otras situaciones de interés.

Ley de Newton de los esfuerzos: el fluido Newtoniano

En todos los fluidos reales existen fuerzas de fricción que se oponen al movimiento y ocasionan disipación de la energía. Es necesario entonces determinar la forma explícita de dichas fuerzas que debe añadirse a la ecuación (47). La fricción en un fluido está relacionada con una propiedad física denominada viscosidad. Cotidianamente podemos observar cómo se manifiesta esta propiedad en diversas situaciones. En las aspas de un ventilador es común encontrar polvo, a pesar de que podría esperarse que el aire en rápido movimiento lo desplazara. Lo que sucede es que el aire que se encuentra justo sobre la superficie del aspa tiene una velocidad cero relativa al aspa de manera que las partículas finas de polvo no son removidas. Es decir, el aire (y cualquier fluido real) se adhiere a las superficies sólidas por el hecho de tener una viscosidad distinta de cero, por lo que una teoría que pretenda describir a los fluidos reales debe considerar este hecho. En un fluido incompresible (i.e. un fluido con densidad constante), la viscosidad está involucrada con los esfuerzos cortantes presentes en un fluido en movimiento. Para cuantificar el efecto de estos esfuerzos, consideremos el siguiente experimento. Supongamos que tenemos dos superficies sólidas planas y paralelas con una capa de agua entre ellas, como se muestra en la figura Fig. 34.

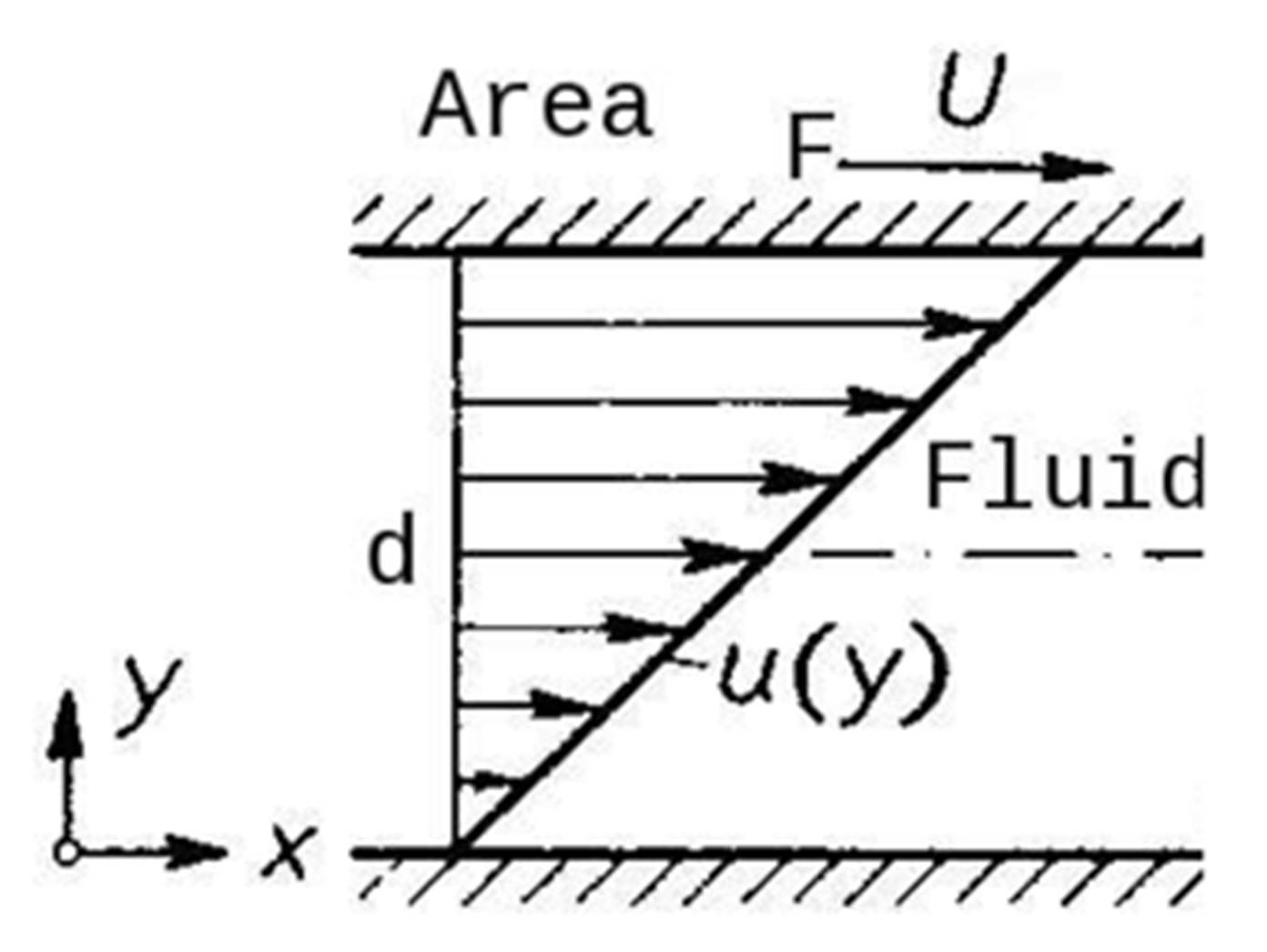
Fig. 34 Fluido viscoso confinado entre dos superficies sólidas planas y paralelas. La superficie superior se desplaza en dirección \(x\) con velocidad \(U\).

La superficie inferior se encuentra fija mientras que la superior, que descansa en la capa de líquido, puede desplazarse en dirección \(x\) paralelamente a la superficie inferior, digamos, con una rapidez \(U\). Si medimos la fuerza requerida para mantener la placa superior en movimiento, encontraremos que mientras más grande sea el área de la placa, \(A\), tendremos que aplicar mayor fuerza y que mientras mayor sea la distancia de separación entre las placas, \(d\), se requerirá una fuerza menor. Por supuesto, mientras mayor sea la velocidad \(U\) también requeriremos aumentar la fuerza. Dicho de otro modo, la fuerza tangencial \(F_x\) es proporcional al área y a la velocidad e inversamente proporcional a la distancia de separación entre las placas, es decir,

\[F_x \quad \propto \quad A \frac{U}{d},\]

Entonces, la fuerza tangencial por unidad de área puede expresarse en la forma:

(58)\[F_x = \mu A \frac{U}{d},\]

donde el coeficiente de proporcionalidad \(\mu\) se conoce como la viscosidad dinámica del fluido y es una propiedad característica de cada sustancia que se determina experimentalmente. Los fluidos que se comportan de acuerdo a la ecuación (58) se conocen como fluidos Newtonianos. De acuerdo con esta ecuación, vemos que las unidades de la viscosidad son N-s/m\(^2\). En ocasiones, en vez de \(\mu\) se utiliza la viscosidad cinemática, definida como \(\nu = \mu/\rho\), que tiene unidades de m\(^2\)/s. En general, la viscosidad depende de la temperatura, sin embargo, para las aplicaciones que estudiaremos aquí, la consideraremos constante.

Notemos que el lado izquierdo de la ecuación (58) es precisamente el esfuerzo cortante en dirección \(x\) aplicado sobre una superficie cuya normal está en dirección \(y\); este esfuerzo se denota comúnmente como \(\sigma_{xy}\). Podemos efectuar un análisis similar al realizado, usando las dos placas sólidas en una pequeña celda rectangular plana dentro del fluido con sus caras paralelas a las direcciónes \(x\) y \(y\), como se muestra en la figura \ref{zoom}.

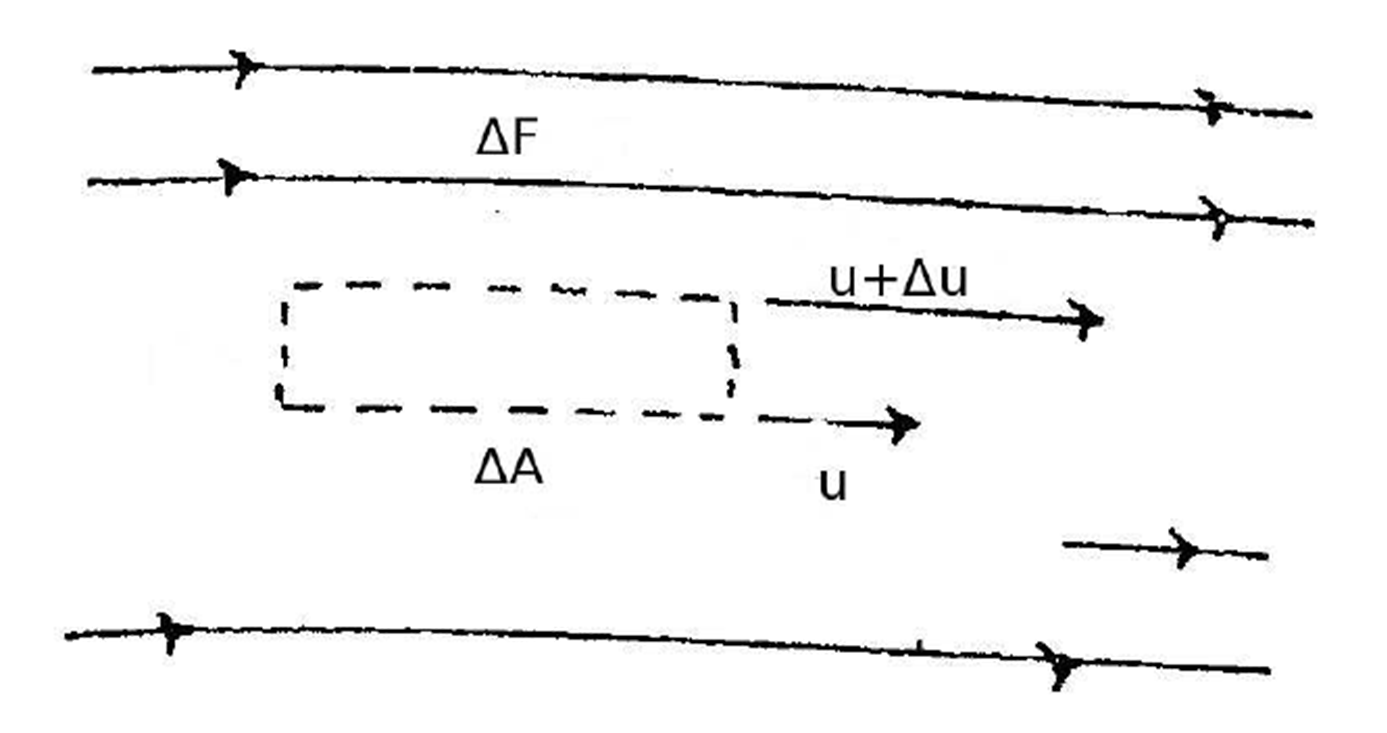
Fig. 35 Esfuerzos cortantes aplicados sobre un volumen de control inmerso en el fluido.

Entonces, si existe un flujo en dirección \(x\), el esfuerzo cortante en esta dirección aplicado sobre la cara con normal en dirección \(y\) se puede expresar como:

\[\sigma_x = \mu \frac{\Delta u}{\Delta y},\]

donde \(u\) es la componente de la velocidad del fluido en dirección \(x\). En el límite en el que el volumen de control es infinitesimal, en un fluido Newtoniano tenemos

(59)\[\sigma_{yx} = \mu \frac{\partial u}{\partial y}.\]

Notemos que para determinar los esfuerzos debemos especificar tanto la dirección en la que se aplica como la dirección normal a la superficie en cuestión. Esto quiere decir que, adicionalmente al esfuerzo \(\sigma_{xy}\), en la cara cuya normal está en dirección \(y\) existirán los esfuerzos \(\sigma_{zy}\) y \(\sigma_{yy}\). Los esfuerzos \(\sigma_{xy}\) y \(\sigma_{zy}\) son cortantes mientras que \(\sigma_{yy}\) es un esfuerzo normal. Como mencionamos previamente, en cada cara del volumen de control existirán dos esfuerzos cortantes y uno normal, dando un total de nueve componentes del esfuerzo, seis cortantes y tres normales, que constituyen el tensor de esfuerzos mecánico.

Puede demostrarse que \(\tilde{{\boldsymbol \sigma}}\) es un tensor simétrico, por lo que \(\sigma_{xy}=\sigma_{yx}\), \(\sigma_{xz}=\sigma_{zx}\) y \(\sigma_{zy}=\sigma_{yz}\), de manera que sólo existen seis componentes independientes. La razón física detrás de la simetría del tensor de esfuerzos es la conservación del momento angular. Si los esfuerzos no fueran simétricos, por ejemplo, si \(\sigma_{xy} \neq \sigma_{yx}\) (ver figura Fig. 32), un elemento de volumen de fluido sería capaz de rotar espontáneamente debido a que los esfuerzos no se equilibrarían. La forma explícita de todas las componentes del tensor \(\tilde{{\boldsymbol \sigma}}\) en términos de las derivadas del campo de velocidad no la mostratremos aquí, pero puede encontrarse en diversos libros de texto.

Debe notarse que el conocer el esfuerzo cortante ejercido por el fluido sobre una pared sólida nos permite conocer la fuerza cortante o tangencial por unidad de área que está actuando sobre dicha pared. Si conocemos el área de la pared podemos entonces determinar la fuerza neta sobre ella.

Ahora queremos determinar la fuerza viscosa por unidad de volumen para sustituirla en la ecuación de balance de momento (47) y obtener la ecuación de movimiento para un fluido real. Aunque la derivación explícita se omitirá por simplicidad, veremos cómo se da el balance de momento en un caso especial y de ahí inferiremos el caso general. Consideremos un flujo bidimensional, en donde todo el fluido se mueve en una sola dirección, digamos de izquierda a derecha en dirección \(x\), como ocurriría en un flujo entre dos paredes paralelas. Para que este flujo tenga lugar, la presión en el extremo izquierdo debe ser mayor que en el extremo derecho. Dicha presión podría ser proporcionada por una bomba mecánica, o bien, por un tinaco que se encuentra en la parte alta y alimenta el ducto por donde fluye el fluido. Por simplicidad, no consideramos la gravedad por el momento. Si observamos el lado derecho de la ecuación (47), vemos que existe un balance entre las fuerzas de presión que impulsan al flujo y las fuerzas viscosas que lo frenan o retardan. Supongamos que el flujo es estacionario, de modo que el campo de velocidades es de la forma \({\boldsymbol u} = (u(y), 0,0)\), donde \(y\) es la coordenada en dirección transversal al flujo, por lo que se trata de un flujo cortante. En tal caso, la aceleración en el fluido es nula

\[a_x = \cancel{\frac{\partial u}{\partial t}} + u\cancel{\frac{\partial u}{\partial x}} = 0\]

Consideremos ahora un volumen de control que encierra una pequeña porción de fluido cuya longitud es \(\delta x\) y su altura \(\delta y\), como el mostrado en la figura Fig. 36.

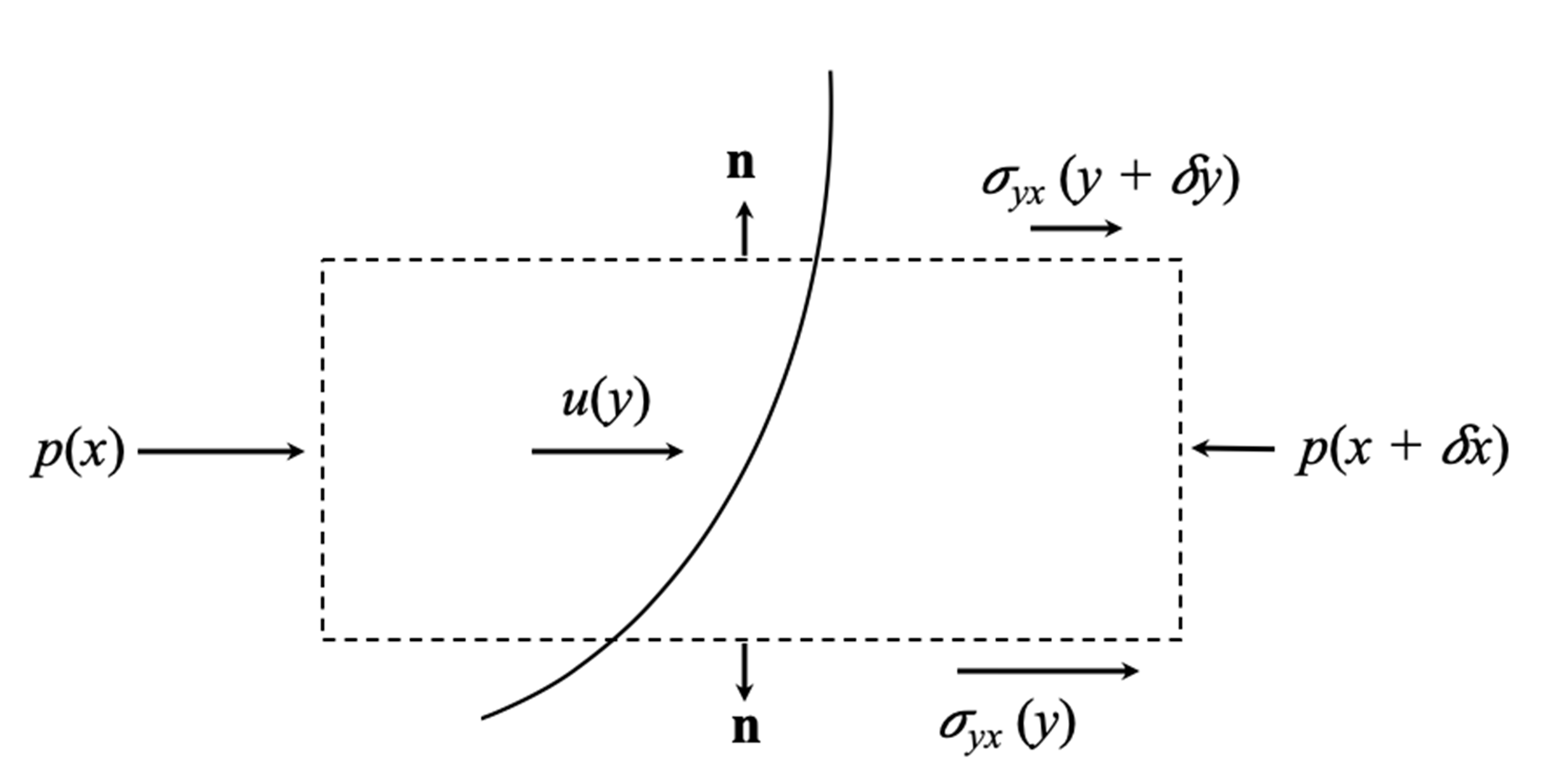
Fig. 36 Las componentes de los esfuerzos de presión y cortantes ejercidos sobre una peque~na porción rectangular de longitud \(\delta x\) y altura \(\delta y\) en un flujo cortante paralelo \(u(y)\) en dirección \(x\).

Mientras que las caras verticales del volumen de control experimentan fuerzas de presión en dirección \(x\), las caras horizontales experimentan esfuerzos cortantes tangenciales en dirección \(x\) debido al fluido circundante. Ya que la aceleración en el fluido es cero, las fuerzas en el volumen de control deben balancearse, entonces

(60)\[p(x)\delta y - p(x+\delta x) \delta y + \sigma_{yx}(y+\delta y) \delta x + \sigma_{yx}(y) \delta x =0.\]

Notemos que la normal en la superficie superior del volumen de control apunta hacia el fluido circundante en dirección \(y\) positiva, mientras que la normal en la superficie inferior apunta hacia el fluido circundante en dirección \(y\) negativa. Recordando la forma explícita de los esfuerzos tangenciales dada por la ley de Newton (59), tenemos entonces que en la cara superior:

(61)\[\sigma_{yx}(y+\delta y) = \mu \frac{\partial u}{\partial y}(y+\delta y).\]

mientras que en la cara inferior

(62)\[\sigma_{yx}(y) = -\mu \frac{\partial u}{\partial y}(y).\]

Por tanto, sustituyendo en la ecuación (60) y dividiendo entre \(\delta x \delta y\), se encuentra

\[\frac{\mu \frac{\partial u}{\partial y}(y+\delta y) -\mu \frac{\partial u}{\partial y}(y) }{\delta y} - \frac{p(x+\delta x) -p(x)}{\delta x} =0 . \]

Tomando los límites \(\delta x \rightarrow 0\) y \(\delta y \rightarrow 0\), obtenemos:

\[\mu \frac{\partial^2 u}{\partial y^2} = \frac{\partial p}{\partial x}. \]

Si seguimos el mismo procedimiento para resolver las fuerzas en la dirección \(y\), encontramos que:

\[0= \frac{\partial p}{\partial y} \]

ya que no existen esfuerzos cortantes en dirección \(y\). Si ahora permitimos que el flujo dependa del tiempo, es decir, \({\boldsymbol u} =(u(y,t),0,0)\) e incluimos la fuerza de cuerpo gravitacional por unidad de volumen \({\bf f}_g = (0,-\rho g,0)\), podemos mostrar que realizando el balance de momento se encuentra:

\[\rho \frac{\partial u}{\partial t} = \mu \frac{\partial^2 u}{\partial y^2} - \frac{\partial p}{\partial x}, \]

\[0= - \frac{\partial p}{\partial y} - \rho g,\]

Estos ejemplos simplificados nos muestran que la fuerza viscosa involucra a las segundas derivadas del campo de velocidades. En el caso general, puede demostrarse formalmente que, para un fluido Newtoniano incompresible, la fuerza viscosa por unidad de volumen tiene la forma:

(63)\[{\bf f}_{visc} = \mu {\boldsymbol \nabla}^2 {\boldsymbol u}.\]

donde aparece el operador Laplaciano:

\[{\boldsymbol \nabla}^2 = \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2} + \frac{\partial^2 }{\partial z^2}. \]

La ecuación de Navier-Stokes

Podemos entonces escribir las ecuaciones que gobiernan el movimiento de un fluido Newtoniano incompresible, es decir,

(64)\[{\boldsymbol \nabla} \cdot {\boldsymbol u}=0,\]

(65)\[\rho \left( \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u}\cdot {\boldsymbol \nabla}) {\boldsymbol u} \right) = -{\boldsymbol \nabla} p + \mu {\boldsymbol \nabla}^2 {\boldsymbol u} + \rho {\bf g},\]

donde hemos incluido la ecuación de continuidad (64) y sustituido la expresión (63) en la ecuación (47) para obtener (65) que se conoce como la \(\textit{ ecuación de Navier-Stokes}\). Si se considera un fluido compresible aparece un término adicional en esta ecuación, que por el momento no consideraremos. La ecuación de Navier-Stokes es la expresión de la segunda ley de Newton para un fluido real. El lado izquierdo de la ecuación (65) representa el producto de la masa por unidad de volumen por la aceleración del fluido. Por su parte, del lado derecho tenemos las distintas fuerzas que actúan sobre el fluido, a saber, la fuerza de presión, la fuerza viscosa y la fuerza gravitacional. Notemos que (65) es una ecuación vectorial, es decir, en general tiene tres componentes. Si reducimos el problema a dos dimensiones, las componentes \(x\) y \(y\) de de las ecuaciones (64) y (65) se reducen a:

\[\begin{split}\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} &=0, \\ \rho \left(\frac{\partial u}{\partial t} +u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}\right) &= - \frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) ,\\ \rho \left( \frac{\partial v}{\partial t} +u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} \right) &= - \frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2} \right) - \rho g , \end{split}\]

donde estamos suponiendo que la gravedad actúa en dirección \(y\), es decir, \({\bf f} = (0, -\rho g)\).