El teorema de Bernoulli

Para establecer este teorema consideremos un fluido ideal e incompresible, por lo que está descrito por las siguientes ecuaciones de movimiento:

(180)\[\nabla\cdot \mathbf{u}=0\]

(181)\[\rho\left[\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u} \cdot\nabla\right) \mathbf{u} \right]=-\nabla p+\rho g\]

Ya que la gravedad es conservativa, podemos expresar la como el gradiente de un potencial

(182)\[g=-\nabla\varphi\]

donde \(\varphi=gz\). Podemos entonces reescribir la ecuación de Euler como

(183)\[\left[\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u} \cdot\nabla\right) \mathbf{u} \right]=-\nabla p=-\frac{1}{\rho}\nabla p-\nabla\varphi\]

(184)\[=-\nabla\left(\frac{p}{\rho}+\varphi\right)\]

(185)\[=-\nabla\left(\frac{p}{\rho}+gz\right)\]

Consideremos ahora la siguiente identidad entre los vectores \(a\) y \(b\),

(186)\[\nabla\left(a\cdot b\right)=\left(a\cdot\nabla\right)b+\left(b\cdot\nabla\right)a+a\times\left(\nabla b\right)+b\times\left(\nabla\times a\right)\]

Si ambos vectores son iguales \(a=b=u\), encontramos que

(187)\[\left(\mathbf{u} \cdot \nabla \right) \mathbf{u} = \left(\nabla\times \mathbf{u} \right)\times \mathbf{u} + \nabla\left(\frac{1}{2}u^{2}\right)\]

donde por simplicidad hemos denotado \(\mathbf{u} \cdot \mathbf{u} =u^{2}\). De este modo, la ecuación de Euler toma la forma

(188)\[\frac{\partial \mathbf{u}}{\partial t}+\left(\nabla \times \mathbf{u} \right)\times \mathbf{u}=-\nabla\left(\frac{p}{\rho}+\frac{1}{2}u^{2}+gz\right)\]

Supongamos ahora que el flujo es estacionario, por lo que la ecuación anterior se reduce a

(189)\[\left(\nabla \times \mathbf{u} \right)\times \mathbf{u} =-\nabla H\]

donde hemos definido la función escalar

(190)\[H=\frac{p}{\rho}+\frac{1}{2}u^{2}+gz\]

Si efectuamos el producto punto del vector velocidad \(\mathbf{u}\) y la ecuación (189),obtenemos

(191)\[\left(\mathbf{u} \cdot \nabla \right)H=0\]

ya que \(\mathbf{u} \cdot\left( \nabla \times \mathbf{u} \right)\times \mathbf{u} = 0\). Para interpretar la ecuación (191), recordemos que el vector \(\nabla H\) indica la dirección en la que la función H varía más rápidamente. Al efectuar el producto punto de \(u\) con \(\nabla H\), estamos proyectando la variación de \(H\) en la dirección de las líneas de corriente, por lo que podemos decir que la cantidad \(\left( \mathbf{u} \cdot \nabla \right)H\) es la razón de cambio de \(H\) a lo largo de una línea de corriente. Por lo tanto, la ecuación (191) indica que en un fluido ideal incompresible en flujo estacionario, la cantidad \(H\) es una constante a lo largo de una línea de corriente. Esta aseveración se conoce como el teorema de Bernoulli y comúnmente a la ecuación

(192)\[H=\frac{P}{\rho}+\frac{1}{2}u^{2}+gz=constante\]

se le conoce como la ecuación de Bernoulli. El teorema de Bernoulli también se puede establecer cuando además de estacionario, el flujo es irrotacional, es decir, \(∇×u=0\). En tal caso, la ecuación (189) se reduce a

(193)\[\nabla H=0\]

lo que indica que H es independiente de la posición y del tiempo. Es decir, en un fluido ideal incompresible en flujo estacionario e irrotacional, la cantidad H es una constante en todo el campo de flujo.

En los dos casos descritos arriba, hemos encontrado que la cantidad \(H\) se mantiene constante, es decir, que \(H\) es una cantidad conservada. Para poder interpretarla de manera más sencilla, podemos multiplicar \(H\) por la densidad, encontrando

(194)\[\rho H=p+\frac{1}{2}\rho u^{2}+\rho gz\]

Ya que \(\rho\) es constante, \(\rho H\) es también una cantidad conservada. Notemos que las unidades de la ecuación (194) son energía por unidad de volumen que coinciden con las unidades de presión, por lo que los tres términos del lado derecho se conocen como la presión estática, la presión dinámica y la presión hidrostática, respectivamente. El segundo término del lado derecho es claramente identificable como la energía cinética por unidad de volumen, mientras que el tercer término es la energía potencial por unidad de volumen asociada al campo de fuerza gravitacional, es decir, a la fuerza de cuerpo. Por su parte, el primer término, la presión, puede interpretarse también como una energía potencial por unidad de volumem pero asociada a las fuerzas internas de corto alcance, es decir, a las fuerzas superficie. El hecho de que la suma de estas tres cantidades se mantenga constante manifiesta la conservación de la energía mecánica en un fluido ideal.

Aplicaciones de la ecuación de Bernoulli

Tubo de Pitot

Veamos ahora cómo podemos utilizar la ecuación de Bernoulli en la resolución de problemas. Una de las aplicaciones básicas se da en la determinación de la velocidad de flujos utilizando diversos dispositivos. Por ejemplo, consideremos el dispositivo ilustrado en la Fig. 56, conocido como tubo de Pitot simple. Se tiene un fluido de densidad \(\rho\) que fluye por un ducto en el que se inserta un pequeño tubo en forma de escuadra con la apertura apuntando hacia donde proviene el flujo. Así, el fluido penetra en el tubo en escuadra quedando estancado y alcanzando una cierta altura \(h\). Si consideramos una

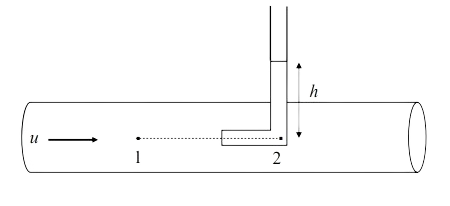
Fig. 56 El tubo de Pitot puede utilizarse para estimar la velocidad promedio del flujo dentro del tubo.

línea de corriente entre los puntos 1 y 2, como se muestra en la Fig. 56, podemos establecer la ecuación de Bernoulli en la forma

(195)\[p_{1}+\frac{1}{2}\rho u_{1}^{2}+\rho gz_{1}=p_{2}+\frac{1}{2}\rho u_{2}^{2}+\rho gz_{2}\]

donde los subíndices indican el punto en donde están asociadas las cantidades. Al aplicar la ecuación de Bernoulli en este problema, debemos considerar que al hablar de presión y velocidad nos referimos a cantidades promedio, no a cantidades locales. Ya que al pasar del punto 1 al 2 nos movemos en la horizontal, tenemos que \(z_{1}=z_{2}\). Además, en el punto 2 el fluido se encuentra estancado por lo que \(u_{2}=0\). Con estas simplificaciones, encontramos

(196)\[p_{1}+\frac{1}{2}\rho u_{1}^{2}=p_{2}\]

lo que muestra que en el punto 2 la presión debe incrementarse para compensar la ausencia de energía cinética. De la ecuación (196), la velocidad en el punto 1 es

(197)\[u_{1}=\sqrt{\frac{2\left(p_{2}-p_{1}\right)}{\rho}}\]

Por otra parte, la diferencia entre las presiones en los puntos 1 y 2 se debe exclusivamente a la columna hidrostática que se encuentra por encima del punto 2, es decir, \(p_{2}-p_{1}=\rho gh\), de manera que

(198)\[u_{1}=\sqrt{\rho gh}\]

Ahora consideremos una ligera variación a la situación anterior, incluyendo una apertura conectada con un tubo vertical por encima del punto 1, donde se forma una pequeña columna estática, como se muestra en la Fig. 57.

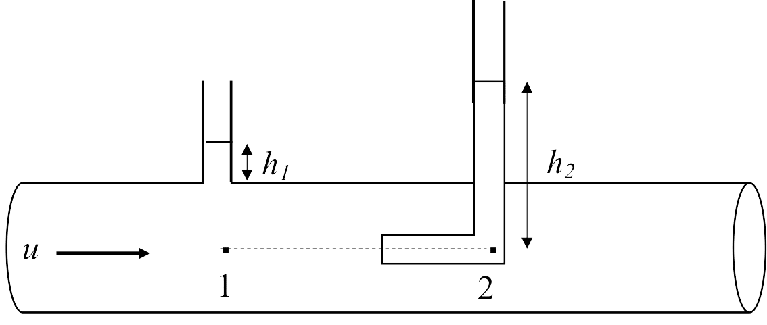
Fig. 57 Flujo en un ducto con una apertura vertical previa a la localización del tubo de Pitot.

La ecuación de Bernoulli entre los puntos 1 y 2 tiene la misma forma que en el caso anterior:

(199)\[p_{1}+\frac{1}{2}\rho u_{1}^{2}=p_{2}\]

sin embargo, ahora la diferencia de presiones entre dichos puntos es \(p_{2}-p_{1}=\rho g\left(h_{2}-h_{1}\right)\), de manera que la velocidad en el punto 1 se expresa como

(200)\[u_{1}=\sqrt{2g\left(h_{2}-h_{1}\right)}\]

Podemos preguntarnos cómo se relacionan las alturas \(h\) y \(h_{2}\) alcanzadas en los tubos de Pitot en los dos casos anteriores. Ya que la velocidad media en ambos casos es la misma, tenemos

(201)\[2gh=2g\left(h_{2}-h_{1}\right)\]

de donde \(h_{2}=h+h_{1}\), es decir, la columna hidrostática en el segundo caso es mayor que en el primero.

Tubo de Venturi

Consideremos otro dispositivo conocido como tubo de Venturi que también permite estimar el gasto o caudal que fluye por una tubería. El dispositivo consiste en un tubo con una reducción de la sección transversal por donde fluye un fluido de densidad \(\rho\), como se muestra en la Fig. 58. En la parte inferior se encuentra un tubo en forma de \(U\) que conecta ambas secciones dentro del cual se dispone un fluido de una densidad \(\rho_{o}\), diferente a la del fluido que fluye entre las dos secciones.

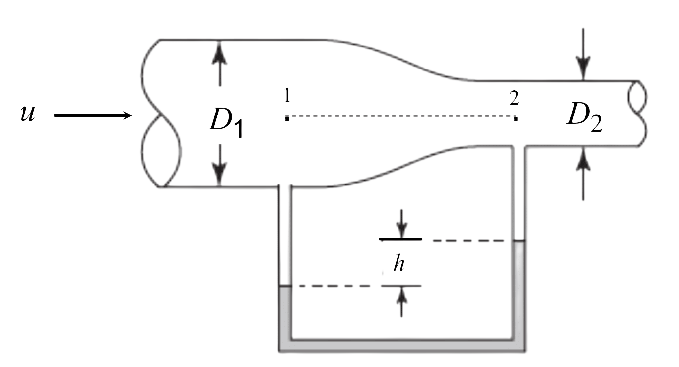
Fig. 58 Tubo de Venturi. Este dispositivo puede utilizarse para estimar la velocidad promedio en el flujo dentro del tubo.

Si planteamos la ecuación de Bernoulli entre los puntos 1 y 2 unidos por una línea de corriente horizontal, tenemos

(202)\[p_{1}+\frac{1}{2}\rho u_{1}^{2}=p_{2}+\frac{1}{2}\rho u_{2}^{2}\]

Debido a la reducción en el área transversal del tubo, la velocidad en el punto 2 será mayor que en el 1, mientras que la presión será menor. La mayor presión estática en el punto 1 ocasiona que el fluido estancado en el tubo en U se desplace hacia la izquierda, causando una diferencia de alturas, \(h\), entre las columnas izquierda y derecha. Para determinar la velocidad media en el tubo debemos considerar también la ecuación de continuidad o conservación del gasto volumétrico, es decir,

(203)\[u_{1}A_{1}=u_{2}A_{2}\]

donde \(A_{1}=\pi D_{1}^{2}/4\) y \(A_{1}=\pi D_{2}^{2}/4\) son las áreas transversales del tubo con diámetros \(D_{1}\) y \(D_{2}\). Tenemos entonces que

(204)\[u_{1}=u_{2}\left(A_{2}/A_{1}\right)\]

y sustituyendo en la ecuación de Bernoulli

(205)\[\frac{1}{2}\rho u_{2}^{2}\left[1-\left(\frac{A_{2}}{A_{1}}\right)^{2}\right]=p_{1}-p_{2}\]

de donde encontramos

(206)\[u_{2}=\sqrt{\frac{2\left(p_1-p_2\right)/\rho}{\left[1-\left(A_{2}/A_{1}\right)^{2}\right]}}\]

La diferencia de presiones corresponde a la presión de la columna de fluido con densidad \(\rho\), de es decir, \(p_{1}-p_{2}=\rho_{o}gh\), la cual es positiva \(\left(p_{1}>p_{2}\right)\). Finalmente, la velocidad media en el punto 2 es

(207)\[u_{2}=\sqrt{\frac{2\left(\rho_{0}/\rho\right)h}{\left[1-\left(A_{2}/A_{1}\right)^{2}\right]}}\]

de manera que el gasto másico está dado por \( \dot{m} = \rho u^2A^2\). Evidentemente, usando la ecuación de continuidad podemos obtener la velocidad media \(u_{1}\).

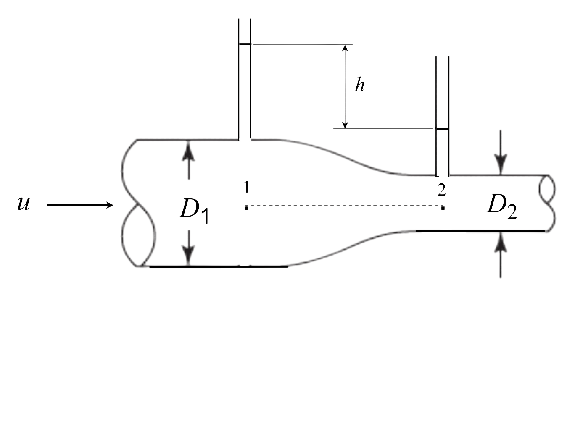
Fig. 59 Variación del tubo de Venturi en donde no interviene un fluido distinto al que fluye por el tubo.

La Fig. 59 ilustra una variación del tubo de Venturi en donde no interviene un segundo fluido. Por encima de los puntos 1 y 2 se localizan tubos verticales dentro de los cuales se estanca el fluido alcanzando un cierta altura. Puesto que en el punto 1 la velocidad es menor que en la sección reducida, la presión estática será mayor que en el punto 2 por lo que la columna de fluido alcanzará una altura mayor. Haciendo un análisis similar al del caso anterior, podemos obtener una expresión para la velocidad media o el gasto en términos de la diferencia de alturas h entre las columnas de fluido.

Vaciado de un recipiente

Analicemos ahora un problema muy común, a saber, el de un contenedor de agua, por ejemplo un tinaco, en cuya parte inferior se encuentra un orificio por donde el agua es desalojada, como se muestra en la Fig. 60. Para simplificar el problema, supongamos primero que mientras que el agua sale por la parte baja, se suministra agua por la parte alta de manera que el nivel de agua del tinaco se mantiene constante. Nos interesa conocer el gasto de agua que sale por el orificio inferior. Si despreciamos las pérdidas viscosas y tratamos al fluido como ideal, podemos aplicar la ecuación de Bernoulli entre el punto 1, localizado en la superficie libre del agua, y el punto 2, a la salida del orificio inferior, es decir,

(208)\[p_{1}+\frac{1}{2}\rho u_{1}^{2}+\rho gz_{1}=p_{2}+\frac{1}{2}\rho u_{2}^{2}+\rho gz_{2}\]

Notemos que ambos puntos se localizan en contacto con la atmósfera de manera que \(p_{1}=p_{2}=p_{atm}\). Además, ya que el nivel de agua en el tinaco se mantiene constante podemos asumir que \(u_{1}=0\), por lo que la velocidad media en el punto 2 es

(209)\[u_{2}=\sqrt{2g\left(z_{1}-z_{2}\right)}=\sqrt{2gh}\]

Si el área del orificio de salida es \(A_{2}=\pi R_{2}^{2}\), donde \(R_{2}\) es el radio de dicho orificio, el gasto volumétrico es

(210)\[Q=u_{2}A_{2}=\pi R_{2}^{2}\sqrt{2gh}\]

Supongamos ahora que el suministro de agua en la parte superior se suprime de manera que el nivel del agua disminuye con el tiempo.

Fig. 60 Tinaco de agua con un orificio de salida en el punto 2. El nivel del agua del tinaco se mantiene constante suministrando el líquido por la parte superior.

En este caso la velocidad en el punto 1 no es cero, sin embargo, el gasto volumétrico se conserva de modo que

(211)\[u_{1}A_{1}=u_{2}A_{2}\]

de donde \(u_{1}=\left(A_{2}/A_{1}\right)u_{2}\), siendo \(A_1=\pi R_{1}^{2}\) el área de la base del tinaco con radio \(R_{1}\). Aplicando la ecuación de Bernoulli entre los puntos 1 y 2, encontramos

(212)\[\frac{1}{2}\rho u_{2}^{2}\left[1-\left(\frac{R_{2}}{R_{1}}\right)^{4}\right]=\rho g(z_{1}-z_{2})=pgh\]

por lo que, la velocidad media en el punto 2 es:

(213)\[u_{2}=\sqrt{\frac{2gh}{\left[1-\left(R_{2}/R_{1}\right)^{4}\right]}}\]

Si el radio del orificio de salida es mucho más pequeño que el radio del tinaco, es decir, \(R_{2}\ll R_{1}\), el término \(\left(R_{2}/R_{1}\right)^{4}\ll1\) por lo que puede despreciarse. Esto equivale a la aproximación \(u_{1}\approx0\), por lo que la velocidad de salida se acerca al caso donde el nivel del agua se mantiene constante: \(u_{1}\approx\sqrt{2gh}\). Podemos estimar el error, \(E_{R}\), asociado a esta aproximación mediante el cociente

(214)\[E_{R}=\frac{\sqrt{\frac{2gh}{1-\left(R_{2}/R_{1}\right)^{2}}}}{\sqrt{2gh}}=\frac{1}{\sqrt{1-\left(R_{2}/R_{1}\right)^{4}}}\]

Para un tinaco de 60 cm de radio y un orificio de salida con un radio de 2.5 cm, el error porcentual es del orden de \(10^{-4}\).

Si queremos determinar el tiempo en el que se vaciará el tinaco, debemos determinar la variación de la altura con el tiempo, es decir, \(h(t)\). Para simplificar un poco la notación, supongamos que \(R_{2}\ll R_{1}\) de manera que la velocidad de salida del agua es \(u_{2}=\sqrt{2gh}\), por lo que el gasto másico a través del orificio será

(215)\[m=-\rho u_{2}A_{2}=-\rho\pi R_{2}^{2}\sqrt{2gh}\]

donde el signo menos indica que el fluido sale del volumen de control. Por otro lado, la masa de agua contenida en el tinaco por encima del nivel del orifico a un instante dado es

(216)\[m=\rho A_{1}h=\rho\pi R_{1}^{2}h\]

por lo que la variación temporal de la masa dentro del tinaco será

(217)\[\frac{dm}{dt}=\frac{d}{dt}\left(\rho\pi R_{1}^{2}h\right)=\rho\pi R_{1}^{2}\frac{dh}{dt}\]

Obviamente, la variación de la masa en el tinaco debe ser igual a la masa desalojada por el orificio, de modo que igualando las ecuaciones (215) y (217), tenemos

(218)\[\rho\pi R_{1}^{2}\frac{dh}{dt}=-\rho\pi R_{2}^{2}\sqrt{2gh}\]

o bien

(219)\[\frac{dh}{dt}=-\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{2gh}\]

Separando esta ecuación e integrando

(220)\[\int\frac{dh}{\sqrt{h}}=-\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{2g}\int dt\]

obtenemos

(221)\[\int\frac{dh}{\sqrt{h}}=-\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{2g}t+C\]

donde \(C\) es una constante de integración que debe determinarse con la condición inicial. Suponiendo que al tiempo \(t = 0\) la altura de la columna por encima del nivel del orificio es \(h = h_{0}\), encontramos \(C=2\sqrt{h_{0}}\), de donde

(222)\[h\left(t\right)=\left[\sqrt{h_{0}}-\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{\frac{g}{2}}t\right]^{2}\]

(223)\[=\frac{1}{2}\left(\frac{R_{2}}{R_{1}}\right)^{4}gt^{2}-\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{2gh_{0}}t+h_{0}\]

Con este resultado podemos obtener la velocidad de salida como función del tiempo, es decir,

(224)\[u_{2}\left(t\right)=\sqrt{2gh\left(t\right)}=\sqrt{2gh_{0}}-\left(\frac{R_{2}}{R_{1}}\right)^{2}gt\]

Finalmente, podemos calcular el tiempo, \(t_{o}\), en el que se vaciará el tinaco, haciendo \(u_{2}(t_{o}) = 0\) o bien \(h(t_{o}) = 0\), es decir,

(225)\[t_{0}=\left(\frac{R_{2}}{R_{1}}\right)^{2}\sqrt{\frac{2h_{0}}{g}}\]

Es importante remarcar que estos resultados se obtuvieron bajo la suposición de que el fluido es ideal de modo que las pérdidas viscosas son inexistentes. En una situación real, la velocidad de salida es menor que la que predice el cálculo previo. La principal pérdida se presenta en el orificio de salida y es totalmente dependiente de su geometría. Es decir, la velocidad de salida dependerá del tipo de boquilla por donde se desaloja el líquido. Para aproximar de mejor manera dicha velocidad, en la práctia se usa un coeficiente de descarga, \(C_{d}\), tal que

(226)\[u_{real}=C_{d}u_{ideal}\]

Este coeficiente que evidentemente deber ser menor que 1, toma en cuenta la disminución de la velocidad de descarga debido a las pérdidas viscosas, así como el hecho de que a la salida existe una reducción en la sección efectiva transversal del flujo.

Otra suposición básica utilizada previamente es que la velocidad de salida es igual a \(\sqrt{2gh}\), independientemente del valor de la altura \(h\), lo cual es una aproximación a la situación real. El resultado \(u=\sqrt{2gh}\) se conoce como la ley de Torricelli.

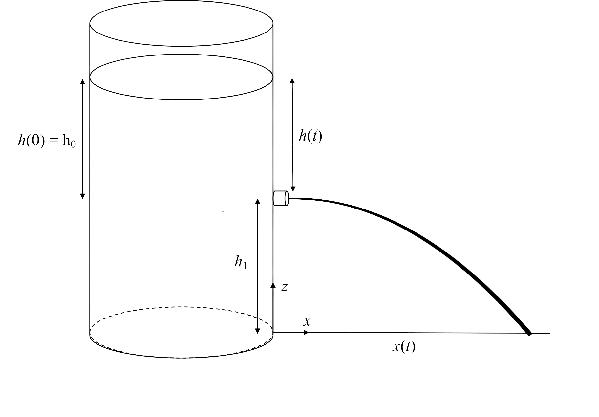
Fig. 61 Tinaco de agua con un orificio de salida a una altura \(h_{1}\) sobre el nivel del piso. El chorro de fluido describe una trayectoria parabólica, mientras que el alcance del chorro disminuye con el tiempo.

Utilicemos los resultados anteriores para analizar una extensión al problema tratado. Consideremos la situación mostrada en la Fig. 61, donde el orificio en el tinaco se localiza a una cierta altura \(h_{1}\) sobre el nivel del piso, de modo que al salir, el chorro de fluido describe una trayectoria parabólica, suponiendo que la interacción con el aire de la atmósfera es despreciable. Inicialmente, la altura de la columna de fluido por encima del nivel de salida es \(h_{0}\), mientras que para \(t>0\) el nivel desciende con el tiempo de acuerdo a la ecuación (223). Nos interesa conocer el alcance máximo del chorro al tocar el piso y cómo este decrece con el tiempo al disminuir el nivel de agua en el tinaco. La trayectoria del chorro está descrita por las ecuaciones del tiro parabólico, es decir,

(227)\[x\left(t\right)=x_{0}+u_{2x}t\]

(228)\[y\left(t\right)=y_{0}+u_{2y}t-\frac{1}{2}gt^{2}\]

donde \(x_{0}\) y \(y_{0}\) son las coordenadas de la posición de salida del chorro, de modo que si colocamos el sistema coordenado en el piso justo en el borde del tinaco, tenemos \(x_{0}=0\) y \(y_{0}=h_{1}\). Por otra parte, \(u_{2x}\) y \(u_{2y}\) son las componentes de la velocidad del chorro a la salida en las direcciones \(x\) y \(y\), respectivamente. Puesto que el chorro sale de forma horizontal, tenemos que \(u_{2x}=\sqrt{2gh\left(t\right)}\) y \(u_{2y} = 0\).

El tiempo, \(t_{1}\), que tarda en tocar el piso una parcela de fluido que sale de la boquilla, se puede calcular haciendo \(y(t_{1}) = 0\), de donde

(229)\[t_{1}=\sqrt{\frac{2h_{1}}{g}}\]

por lo que el alcance del chorro es

(230)\[x\left(t\right)=u_{2x}\left(t\right)t1=u_{2x}\left(t\right)\sqrt{\frac{2h_{1}}{g}}\]

Pero la velocidad \(u_{2x}(t)\) es justamente la que calculamos con la ecuación de Benoulli. Bajo la suposición \(R_{2}\ll R_{1}\), tenemos

(231)\[u_{2x}=\sqrt{2gh\left(t\right)}\]

de manera que utilizando la ecuación (223), el alcance puede expresarse como

(232)\[x\left(t\right)=\sqrt{\frac{2h_{1}}{g}}\sqrt{2g}\left[\sqrt{h_{0}}\left(\frac{R1}{R2}\right)^{2}\sqrt{\frac{g}{2}}t\right]\]

(233)\[=\sqrt{4h_{1}}\left[\sqrt{h_{0}}-\left(\frac{R1}{R2}\right)^{2}\sqrt{\frac{g}{2}}t\right]\]

El alcance máximo se obiente en \(t = 0\), cuando el nivel de agua en el tinaco es el más alto:

(234)\[x_{max}=\sqrt{4h_{0}h_{1}}\]

Derivación alternativa de la ecuación de Bernoulli

Veamos ahora una manera alternativa de derivar la ecuación de Bernoulli analizando el movimiento de una partícula cúbica de fluido que se desplaza de izquierda a derecha sujeta a un gradiente de presión a lo largo de una línea de corriente, como se muestra en la Fig. 62. La partícula de masa \(m\) experimenta una presión \(p\) en la cara trasera y una presión \(p+dp\) en la delantera. De acuerdo a la segunda ley de Newton tenemos

(235)\[F=ma=m\frac{du}{dt}\]

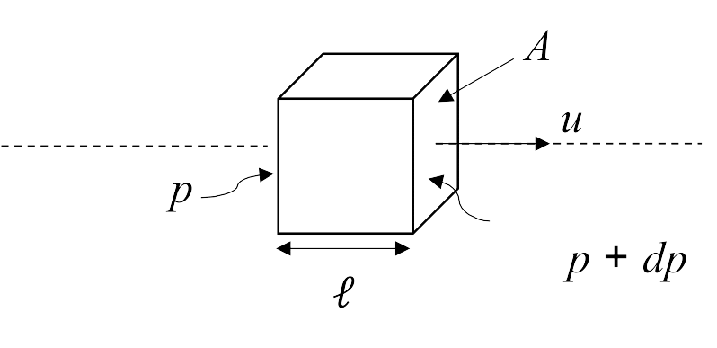
Fig. 62 Partícula de fluido a lo largo de una línea de corriente

donde \(a\) y \(u\) son la acelaración y la velocidad de la partícula y la fuerza resultante F está dada por

(236)\[F=pA-\left(p+dp\right)dA=-Adp\]

donde \(A\) es el ára de las caras del cubo. A su vez, la masa de la partícula se puede expresar en la forma

(237)\[m=\rho A\ell\]

donde \(\rho\) es la densidad del fluido y \(\ell\) es la longitud de la cara del cubo. Por otra parte, la magnitud del cambio de presión entre la superficie frontal y la trasera se puede aproximar a partir del gradiente de presión longitudinal \(dp/dx\), de modo que

(238)\[dp\thickapprox\frac{dp}{dx}\Delta x=\ell\frac{dp}{dx}\]

ya que \(\Delta x=\ell\). Sustituyendo en la segunda ley de Newton tenemos

(239)\[-\ell\frac{dp}{dx}A=\ell A\rho\frac{du}{dt}\]

o bien

(240)\[dp=-\rho\frac{du}{dt}dx=-\rho\frac{dx}{dt}du\]

pero \(dx/dt = u\) de modo que podemos escribir

(241)\[dp=-\rho udu\]

Podemos ahora integrar entre dos puntos 1 y 2 que se encuentren a lo largo de la línea de corriente para relacionar la diferencia de presiones con la diferencia de velocidades entre los puntos, es decir

(242)\[\intop_{1}^{2}dp=-\int_{1}^{2}\rho udu\]

de donde obtenemos

(243)\[p_{2}-p_{1}=-\left(\rho\frac{u_{1}^{2}}{2}-\rho\frac{u_{1}^{2}}{2}\right)\]

o bien

(244)\[p_{1}+\rho\frac{u_{1}^{2}}{2}=p_{2}+\rho\frac{u_{2}^{2}}{2}\]

Ya que los puntos 1 y 2 son arbitrarios, la ecuación (244) puede utilizarse para conectar cualesquiera dos posiciones a lo largo de una línea de corriente. Evidentemente se trata de la ecuación en donde se ha omitido el término de energía potencial por simplicidad.

Gradiente de presión a través de líneas de corriente curvas

Ahora analicemos la forma en que varía el gradiente de presión cuando nos movemos transversalmente a líneas de corriente [9]. Consideremos una partícula de fluido que se desplaza sobre una línea de corriente curva, como la mostrada en la Fig. 63. La fuerza centrípeta que se ejerce sobre una

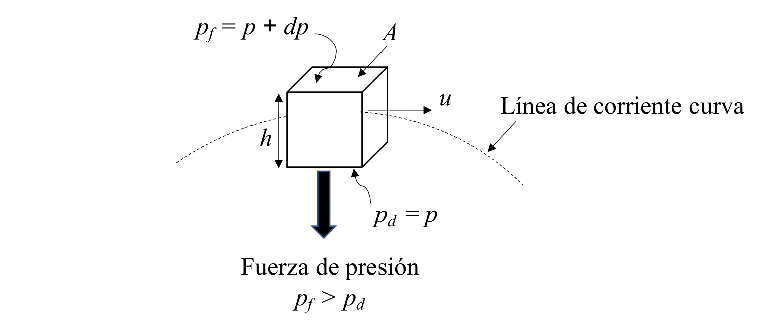
Fig. 63 Variación de la presión en dirección transversal a una línea de corriente curva.

partícula de masa \(m\) que se mueve siguiendo una trayectoria curva está dada por

(245)\[F=m\frac{u^{2}}{R}\]

donde \(R\) es el radio de curvatura local. En términos de la densidad, la masa puede expresarse como \(m=\rho Ah\), donde \(A\) es el área de la cara y \(h\) la altura del cubo. Si la presión en la cara inferior del cubo es

(246)\[p_{i}=p\]

y en la cara superior es

(247)\[p_{s}=p+dp\]

podemos aproximar la diferencial de la presión en la forma

(248)\[dp\approx h\frac{dp}{dn}\]

donde \(n\) es la coordenada en la dirección normal a la línea de corriente y apunta alejándose del centro de curvatura. Combinando estas ecuaciones, de la ecuación (245) obtenemos

(249)\[F=Adp=Ah\frac{dp}{dn}=\rho Ah\frac{u^{2}}{R}\]

de donde

(250)\[\frac{dp}{dn}=\rho\frac{u^{2}}{R}\]

Esta ecuación nos dice que sobre una partícula de fluido que sigue una trayectroria curva, existe una fuerza centrípeta que actúa normal a la dirección de movimiento. En particular, expresa que el gradiente de presión a través de las líneas de corriente depende del radio de curvatura local \(R\), y la velocidad \(u\). Si la línea de corriente es recta de modo que \(R\rightarrow\infty\), tenemos que

(251)\[\frac{dp}{dn}=0\]

por lo que no existe gradiente de presión en la dirección transversal a líneas de corriente sin curvatura. Por el contrario, si una línea de corriente es curva debe existir un gradiente de presión a través de la línea de corriente, incrementándose la presión en la dirección que se aleja del centro de curvatura.

Variación de la presión en un vórtice atmosférico

Esto nos permite entender que en un tornado o un vórtice atmosférico cuyas líneas de corriente son aproximadamente círculos concéntricos, existe un gradiente de presión a través de ellas de tal modo que la presión disminuye conforme nos acercamos al núcleo del vórtice. Esto explica por qué los tornados succionan a los objetos que encuentran a su paso. Si aplicamos la ecuación de Bernoulli a estas líneas de corriente, encontramos que la velocidad se incrementa conforme nos acercamos al núcleo, es decir, el fluido en las líneas de corriente más externas tendrá una mayor presión y menor velocidad que aquel que se encuentre en líneas de corriente más cercanas al núcleo. En los huracanes la velocidad del viento alcanza un máximo en la frontera que divide al núcleo, también llamado ojo del huracán, con el exterior del vórtice [9]. El ojo del huracán es una zona de baja presión y baja velocidad donde los efectos de fricción son importantes.

Fig. 64 Líneas de corriente alrededor de un ala curveada [10].

Empuje sobre un ala

Siguiendo el razonamiento expuesto por H. Babinsky [9], la ecuación (250) también permite entender cómo es que se produce el empuje en un ala de avión con una cierta curvatura. La Fig. 64 muestra las líneas de corriente que se forman alrededor de una ala debido a un flujo de aire que viaja de izquierda a derecha. Las líneas verticales punteadas indican puntos en distintas líneas de corriente lejanos y cercanos al ala. El punto \(A\) se encuentra suficientemente alejado del ala de modo que la presión es la atmosférica, \(P_{A} =P_{atm}\). Además, ya que en la región cercana al punto A las líneas son prácticamente rectas y paralelas, no existe gradiente de presión en la dirección transversal a la línea punteada. Si nos acercamos hacia el ala la curvatura de las líneas de corriente empieza a aumentar por lo que debe existir un gradiente de presión a través de ellas. Dada la curvatura de dichas líneas podemos deducir que la presión desciende conforme nos movemos hacia abajo por lo que en el punto \(B\) la presión debe ser mucho menor que en el \(A\), es decir, \(p_{B} < p_{atm}\). Por otra parte, si nos desplazamos del punto \(C\) al \(D\), conforme nos acercamos al ala, las líneas de corriente tienen mayor curvatura pero en este caso la presión tiende a incrementarse. Por lo tanto, en el punto \(D\) la presión debe ser mayor que en el punto \(C\) donde la presión es esencialmente la atmosférica, es decir, \(p_{D} > p_{atm}\). En consecuencia tenemos que la presión por encima del ala es menor que por debajo de ella, es decir, \(p_{A} < p_{D}\), lo que ocasiona una fuerza de empuje sobre el ala hacia arriba. Así, cualquier superficie que introduce curvatura en el campo de flujo puede generar empuje. Babinsky concluye que las alas funcionan porque el flujo sigue la curvatura local de la superficie tanto en la superficie superior como en la interior [9].