El principio de Pascal

Uno de los principios básicos de la hidrostática es el denominado Principio de Pascal que dice lo siguiente:

Important

La presión ejercida por un fluido incompresible y en equilibrio dentro de un recipiente de paredes indeformables se transmite con igual intensidad en todas las direcciones y en todos los puntos del fluido.

Este principio explica muchos de los comportamientos que observamos en fluidos en reposo. Por ejemplo, consideremos el caso de los vasos comunicantes como el mostrado en la figura Fig. 40 en donde un líquido incompresible llena un recipiente formado por tubos de distinta forma abiertos a la atmósfera.

Observamos que el nivel que alcanza el líquido es el mismo en todos los tubos idependientemente de su forma o inclinación. Evidentemente en la superficie libre del líquido en todos los tubos la presión es la atmosférica mientras que en el fondo la presión será en todos lados la misma y dependerá únicamente de la altura \(h\) de la columna de líquido. Tenemos entonces que en un plano horizontal dentro del fluido, la presión será la misma en cualquier punto del plano.

Consideremos ahora el caso mostrado en la figura Fig. 41, donde tres de los tubos tienen sus extremos superiores sellados mientras que uno de ellos, más alto que los demás, está abierto a la atmósfera. Si vaciamos el líquido a través de este tubo, los tubos cerrados se llenarán hasta alcanzar una altura \(h\), quedándo el aire atrapado en la parte superior de los tubos. La presión del aire atrapado, \(p_{x}\), dependerá de la presión atmosférica y de la altura \(h_{1}\) que alcance el líquido en el tubo abierto a partir del nivel de líquido en los tubos cerrados, es decir, \(p_{atm}+\rho gh_{1}\), mientras que en el fondo la presión será \(p_{x}=p_{atm}+\rho g\left(h_{1}+h\right)\). Esto nos muestra que la presión en un sistema de tuberías se puede incrementar simplemente colocando un tinaco en una torre suficientemente alta.

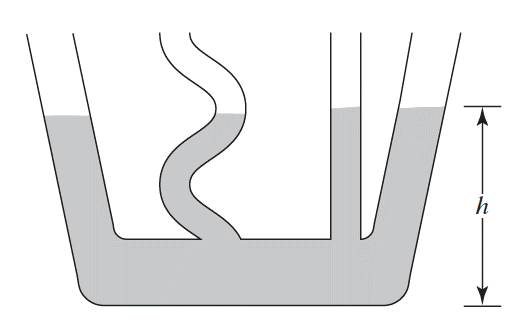
Fig. 40 Vasos comunicantes abiertos a la atmósfera

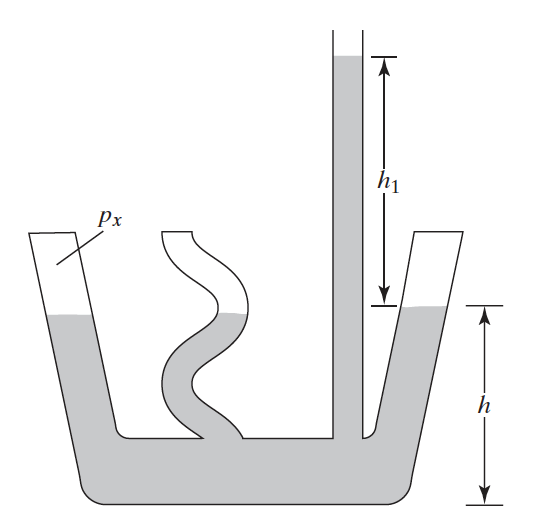
Fig. 41 Vasos comunicantes con tres de los tubos cerrados y uno abierto a la atmósfera.

El pricipio de Pascal se puede utilzar también para medir la presión mediante lo que se conoce como manómetros de tubo en U. Analicemos primero el caso más sencillo mostrado en la figura Fig. 42 , donde nos interesa conocer la presión, \(p_{x}\), en el centro de la cavidad esférica que está llena con un fluido de densidad \(\rho\) que alcanza la altura \(h\) en el tubo que está abierto a la atmósfera. Para esto debemos recorrer del punto \(x\) hasta llegar al punto \(2\). Notemos que el punto \(1\) está a la misma altura que el punto \(x\) por lo que la presión es la misma, es decir, \(p_{x}=p_{1}\). Ahora nos movemos del punto \(1\) al \(2\) lo que ocasiona que la presión disminuya por \(\rho gh\) y justo en el punto \(2\) la presión es la atmosférica, es decir,

(89)\[p_{x}-\rho gh=p_{atm}\]

de donde

(90)\[px=p_{atm}+\rho gh\]

Ahora consideremos el manómetro de la figura Fig. 43 donde queremos conocer la presión \(p_{x}\) en la cavidad esférica que se encuentra llena de un fluido de densidad \(\rho_{1}\). Primero notemos que los puntos que están a la misma altura tienen presiones iguales, es decir, \(p_{x}=p_{1}\) y \(p_{2}=p_{3}\). Al recorrer del punto \(1\) al \(2\) aumentamos la presión por \(\rho_{1}gh_{1}\) y luego al ir del \(2\) al \(3\) no cambia la presión, mientras que al ir del \(3\) al \(4\) disminuye la presión por \(\rho_{2}gh_{2}\) y se iguala a la presión atmosférica, entonces

(91)\[p_{x}+\rho_{1}gh_{1}-\rho_{2}gh_{2}=p_{atm}\]

de donde

(92)\[p_{x}=\rho_{2}gh_{2}-\rho_{1}gh_{1}+p_{atm}\]

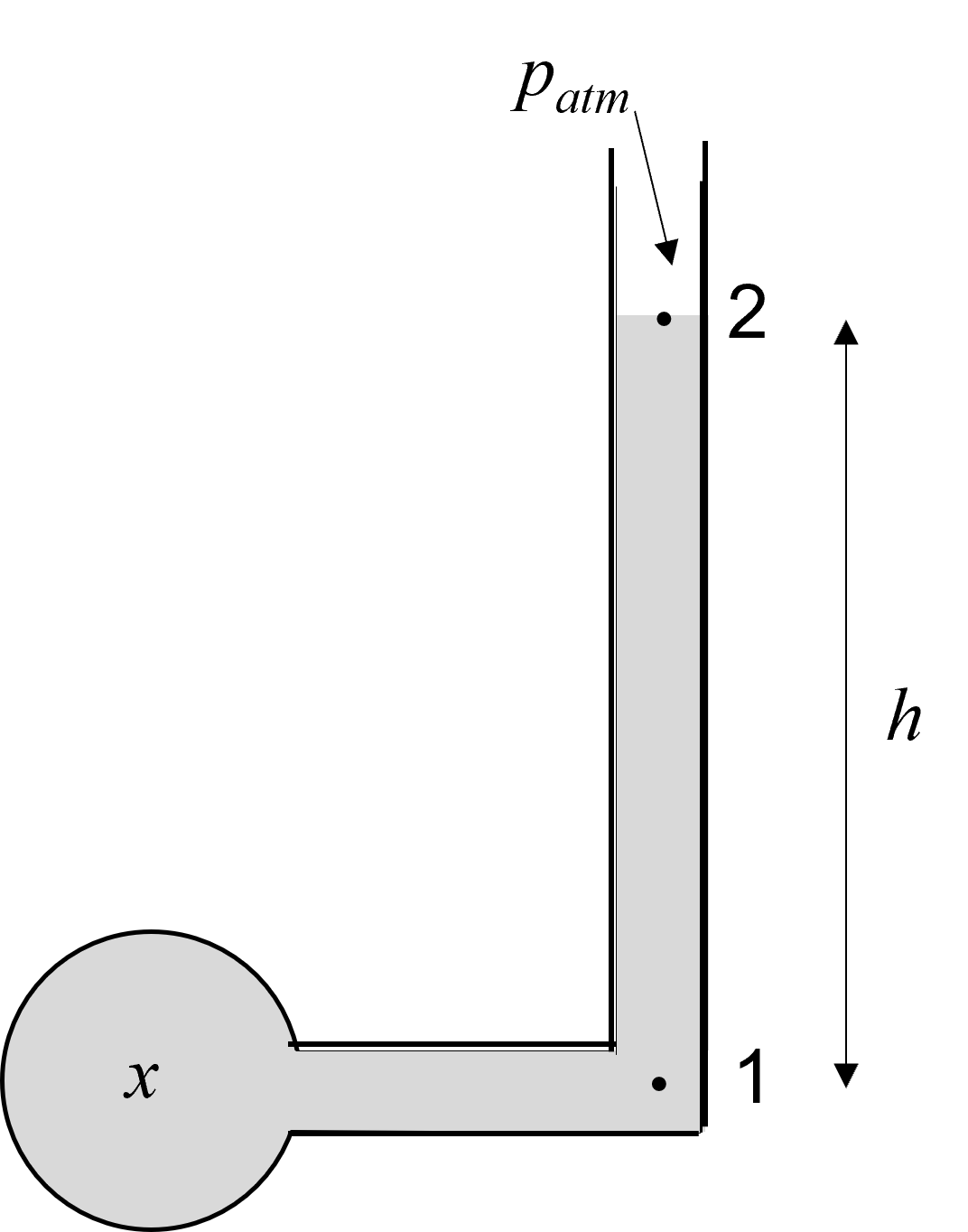
Fig. 42 Manómetro sencillo.

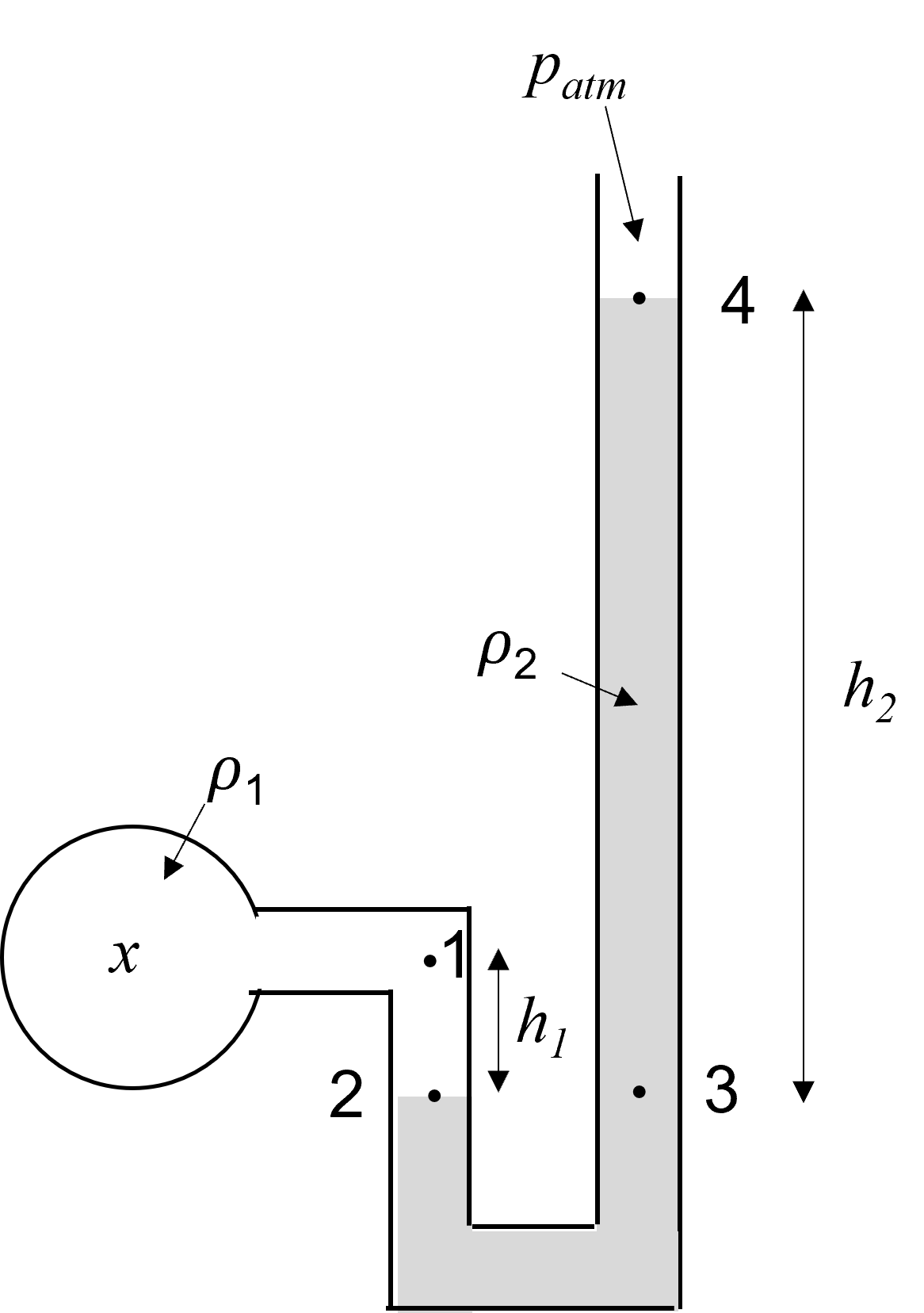
Fig. 43 Manómetro de tubo en U.

La utilidad del principio de Pascal se manifiesta claramente también en otra aplicación tecnológica muy común conocida como gato hidráulico que permite levantar pesos muy grandes aplicando una fuerza comparativamente pequeña. En este dispositivo, mostrado en la figura Fig. 44, dos columnas de fluido con áreas transversales diferentes se encuentran conectadas en la parte baja, mientras que los extremos superiores rígidos de cada de columna se pueden desplazar verticalmente. Al aplicar una fuerza \(F_{1}\) sobre la columna izquierda con área \(A_{1}\), la presión resultante es \(p=F_{1}/A_{1}\). Ya que la presión se transmite a todos los puntos del fluido con igual intensidad, la presión sobre la tapa superior de la columna derecha será la misma, es decir,

(93)\[p\frac{F_{1}}{A_{1}}=\frac{F_{2}}{A_{2}}\]

Por lo tanto, la fuerza ejercida sobre la tapa superior de la columna derecha es

(94)\[F_{2}=F_{1}\frac{A_{2}}{A_{1}}\]

y dado que \(A_{2}>A_{1}\), la fuerza \(F_{2}\) es mayor que \(F_{1}\) por el factor \(A_{2}/A_{1}\). Así, variando las áreas adecuadamente es posible incrementar la fuerza \(F_{2}\) sustancialmente. Dado que la presión dentro del fluido es muy grande, las pequeñas variaciones ocasionadas por la diferencia de alturas de las columnas de fluido se pueden despreciar.

Fig. 44 Gato hidráulico.