Energía eólica: el límite de Betz

La potencia del viento

Consideremos una masa de aire m que se mueve a velocidad \(u\) de manera que su energía cinética es

(252)\[E_{c}=\frac{1}{2}mu^{2}\]

donde \(u\) es la magnitud del vector \(\mathbf{u}\). La masa de aire de densidad \(\rho\) que atraviesa con velocidad \(u\) una sección transversal de área \(A\) en un tiempo \(\Delta t\) es

(253)\[m = \rho V = \rho A u \Delta t\]

donde \(V\) es el volumen de aire en un tiempo \(\Delta t\). Sustituyendo la ecuación (253) en (252) encontramos

(254)\[E_{c}=\frac{1}{2}\rho A\Delta tu^{3}\]

y ya que la energía cinética de la masa de aire por unidad de tiempo es la potencia del viento, tenemos

(255)\[P_{v}=\frac{E_{c}}{\Delta t}=\frac{A}{2}\rho u^{3}\]

o bien, por unidad de área

(256)\[\frac{P_{v}}{A}=\frac{1}{2}\rho u^{3}\]

donde observamos que es proporcional al cubo de la velocidad. Por tanto, para una velocidad del viento de 4 m/s con una densidad del aire de \(1.225\textrm{ kg/m}^{3}\) a \(15°\)C, se tiene una potencia por unidad de área de \(39.2 \textrm{ W/m}^{2}\), mientras que para el doble de velocidad, \(u =8 \textrm{ m/s}\), la densidad de potencia es ocho veces mayor, es decir, \(313.6 \textrm{ W/m}^{2}\). Nótese que el mismo análisis es válido para una corriente marina por lo que, tomando en cuenta la densidad del agua de mar, la potencia se incrermentaría aproximadamente por un factor de 1000.

Potencia transferida por el viento a un rotor

Una cuestión muy importante en el aprovechamiento de la energía eólica es determinar la máxima potencia del viento que es posible extraer mediante un aerogenerador. Para tal fin, haremos algunas simplificaciones, en particular supondremos que el aire es un fluido ideal de manera que despreciaremos los efectos viscosos. Consideremos un tubo de corriente como el mostrado en la Fig. 65 el cual encierra a un rotor o hélice que barre un área transversal \(A\) por donde atraviesa el viento con velocidad promedio \(u\). Por simplicidad podemos obviar las aspas del rotor e imaginarlo como un disco sólido. En el lado izquierdo del tubo de corriente el viento atraviesa una sección transversal de área \(A_{1}\) con una velocidad promedio \(u_{1}\), mientras que en el extremo derecho el viento pasa por una sección de área \(A_{2}\) con una velocidad promedio \(u_{2}\). Ya que parte de la energía cinética del aire es captada por el disco, es esperable que la velocidad detrás del rotor sea menor de modo que la relación entre las magnitudes de las velocidades es \(u_{2}<u<u_{1}\). Evidentemente, la velocidad \(u_{2}\) nunca es cero pues en tal caso la totalidad de la energía cinética del viento sería captada por el rotor, frenando el viento completamente. Si analizamos el flujo mediante la ecuación de Bernoulli, cuando el viento atraviesa el rotor disminuye su velocidad lo que lleva a un incremento en la presión. Además, el gasto másico, \(m\), a través del tubo de corriente debe conservarse, es decir,

(257)\[m=\rho u_{1}A_{1}=\rho u_{2}A_{2}=\rho u A\]

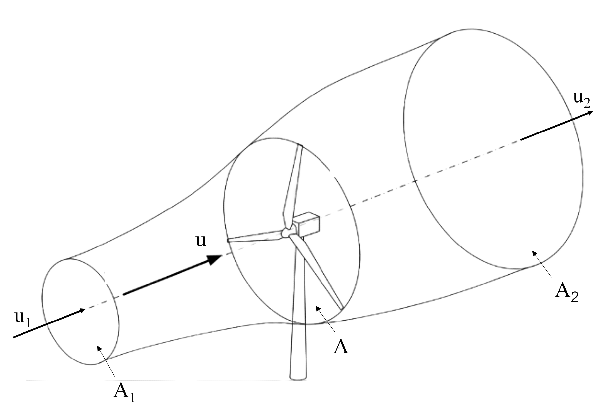
Fig. 65 Tubo de corriente para establecer el límite de Betz

donde hemos supuesto que aire es incompresible de modo que la densidad es constante. Ya que \(u_{2}<u<u_{1}\), la ecuación (257) implica que \(A_{2}<A<A_{1}\). Es decir, el incremento en la presión detrás del rotor lleva a un aumento en el área de la sección transversal del tubo de corriente.

Ahora determinemos de dos maneras distintas, la potencia del viento que puede ser aprovechada por el rotor, \(P_{u}\), que denominaremos la potencia útil. Primero calculemos el cambio por unidad de tiempo en la energía cinética del viento que pasa a través del rotor, es decir,

(258)\[P_{u}=\frac{\Delta E_{c}}{\Delta t}=\frac{1}{2}m(u_{1}^{2}-u_{2}^{2})\]

de donde, al sustituir el gasto másico de la ecuación (257), encontramos

(259)\[Pu=\frac{1}{2}\rho uA\left(u_{1}^{2}-u_{2}^{2}\right)\]

Ahora calculemos \(P_{u}\) de una manera alternativa considerando la fuerza ejercida por el viento sobre el rotor. De la segunda ley de Newton tenemos

(260)\[Pu=\frac{1}{2}\rho uA\left(u_{1}^{2}-u_{2}^{2}\right)\]

por lo que el trabajo hecho por esta fuerza en un desplazamiento dx es \(dW = F dx\). Entonces, la potencia útil se puede calcular como

(261)\[P_{u}=\frac{dW}{dt}=F\frac{dx}{dt}=Fu\]

de donde al sustituir la fuerrza de la ecuación (260), obtenemos

(262)\[P_{u}=\frac{dW}{dt}=F\frac{dx}{dt}=Fu\]

Igualando las expresiones (259) y (262) encontramos

(263)\[\frac{1}{2}\rho uA\left(u_{1}^{2}-u_{2}^{2}\right)=\rho Au^{2}(u_{1}-u_{2})\]

o bien

(264)\[\frac{1}{2}\rho uA\left(u_{1}+u_{2}\right)\left(u_{1}-u_{2}\right)=\rho Au^{2}(u_{1}-u_{2})\]

de donde obtenemos

(265)\[u=\frac{1}{2}\left(u_{1}+u_{2}\right)\]

es decir, la velocidad del viento en el plano del rotor es el promedio de las velocidades en las secciones \(A_{1}\) y \(A_{2}\). Si ahora utilizamos el resultado (265) para calcular la potencia útil, de la ecuación (259) obtenemos

(266)\[P_{u}=\frac{1}{2}\rho A\frac{\left(u_{1}+u_{2}\right)}{2}\left(u_{1}^{2}-u_{2}^{2}\right)\]

Ya que \(u_{2}\) es menor que \(u_{1}\), podemos expresar \(u_{2}=bu_{1}\), donde \(0<b<1\). Al sustituir en (266) encontramos

(267)\[P_{u}\left(b\right)=\frac{1}{2}\rho A\frac{\left(u_{1}+bu_{1}\right)}{2}\left(u_{1}^{2}-b^{2}u_{1}^{2}\right)=\frac{1}{4}\rho Au_{1}^{3}\left(1+b\right)\left(1-b^{2}\right)\]

Si toda la potencia del viento fuera captada por el rotor, \(b = 0\), mientras que si no se transmitiera ninguna potencia al rotor, \(b = 1\). Maximizando la función \(P_{u}(b)\), tenemos

(268)\[\frac{dP_{u}}{db}=0\Longrightarrow\frac{d}{db}\left[\left(1+b\right)\left(1-b^{2}\right)\right]=\left[\left(1+b\right)\left(1-3b\right)\right]=0\]

cuyas raíces son \(b = −1\) y \(b = 1/3\). La raíz \(b = −1\) no tiene sentido físico puesto que \(u_{2}\) debe ser positiva, por tanto encontramos que la velocidad \(u_{2}\) que maximiza la potencia útil es

(269)\[u_{2}=\frac{1}{3}u_{1}\]

Sustituyendo este valor en la ecuación (266) encontramos que la máxima potencia útil que puede ser extraída del viento es

(270)\[P_{u}=\frac{1}{2}\rho Au_{1}^{3}\frac{1}{2}\left(1+\frac{1}{3}\right)\left(1-\frac{1}{9}\right)=\left(\frac{16}{27}\right)\frac{1}{2}\rho Au_{1}^{3}\]

que podemos exprersar como

(271)\[P_{u}=C_{p}\frac{1}{2}\rho Au_{1}^{3}\]

o bien

(272)\[C_{p}=\frac{P_{u}}{P_{v}}\]

donde \(C_{p}=16/27=0.593\) se conoce como el coeficiente de potencia. Esto nos indica que de la potencia disponible del viento, \(P_{v}=ρAu_{1}^{3}/2\), podemos aprovechar como máximo el \(59.3 \%\). Esta restricción en la potencia útil que puede extraerse de un rotor o hélice se conoce como el límite de Betz. Aunque comúnmente este resultado se refiere al aprovechamiento de la energía eólica, su validez se extiende a los generadores marinos. Dado que llegamos a este resultado suponiendo un fluido ideal, es de esperarse que en situaciones reales donde los efectos viscosos están presentes el porcentaje de provechamiento se reduzca aún más.