Descripciones Lagrangiana y Euleriana

Descripciones Lagrangiana y Euleriana

Describir el movimiento de fluidos puede ser una tarea complicada ya que se trata de un medio deformable. Para realizar la descripción de cualquier movimiento debemos iniciar eligiendo un sistema coordenado respecto al cual referimos el desplazamiento del medio.

Esencialmente, existen dos formas en que podemos describir el movimiento de un fluido, conocidas como las descripciones Lagrangiana y Euleriana. Se diferencian básicamente por la forma en que se eligen los volúmenes de control del fluido bajo estudio.

Descripción Lagrangiana

En la descripción Lagrangiana se persigue un volumen de control que se desplaza con el medio, es decir, un volumen de control que no está fijo en el espacio y que contiene siempre a las mismas partículas de fluido. Su desplazamiento se mide respecto al sistema coordenado que elegimos y para analizar el volumen de control particular que estamos considerando, lo etiquetamos o marcamos registrando su posición inicial a un cierto tiempo, de manera semejante a como se hace al describir el movimiento de partículas sólidas.

Nótese que un volumen de control lo puede constituir una sola partícula de fluido que visualizamos como un punto en el espacio. Por ejemplo, supongamos que queremos describir la temperatura de un fluido en movimiento utilizando la descripción Lagrangiana. Elegimos entonces una partícula de fluido que pasa por una cierta posición inicial \({\boldsymbol r}_0 = \left( x_0,y_0,z_0 \right)\) al tiempo \(t=t_0\), por lo que su temperatura a cualquier tiempo posterior, \(t\), la podemos denotar como \(T \left( x_0, y_0, z_0, t \right)\) (ver Fig. 6). Nótese que la cantidad \({\boldsymbol r}_0 = \left(x_0,y_0,z_0 \right)\) es constante. Consideramos que dicha partícula es pasiva dado que su movimiento está dictado completamente por el flujo en el que se encuentra inmerso, de modo que no altera el flujo a su alrededor sino que actúa pasivamente dejándose llevar por el movimiento del fluido. En la práctica, una partícula de polvo suspendida en el aire, una boya en el océano o un globo en la atmósfera, aunque ajenos al fluido, pueden, bajo ciertas condiciones, ser consideradas como partículas pasivas.

En este caso, la variable dependiente (temperatura) es una función de la posición inicial de la partícula elegida y del tiempo, de modo que la temperatura de la partícula puede tomar diversos valores a distintos tiempos conforme el fluido se mueve. Al igual que la temperatura, podemos describir otras variables de interés como la densidad, la presión o la velocidad de la partícula. En general, en la descripción Lagrangiana las variables independientes son la posición inicial de la partícula de fluido y el tiempo.

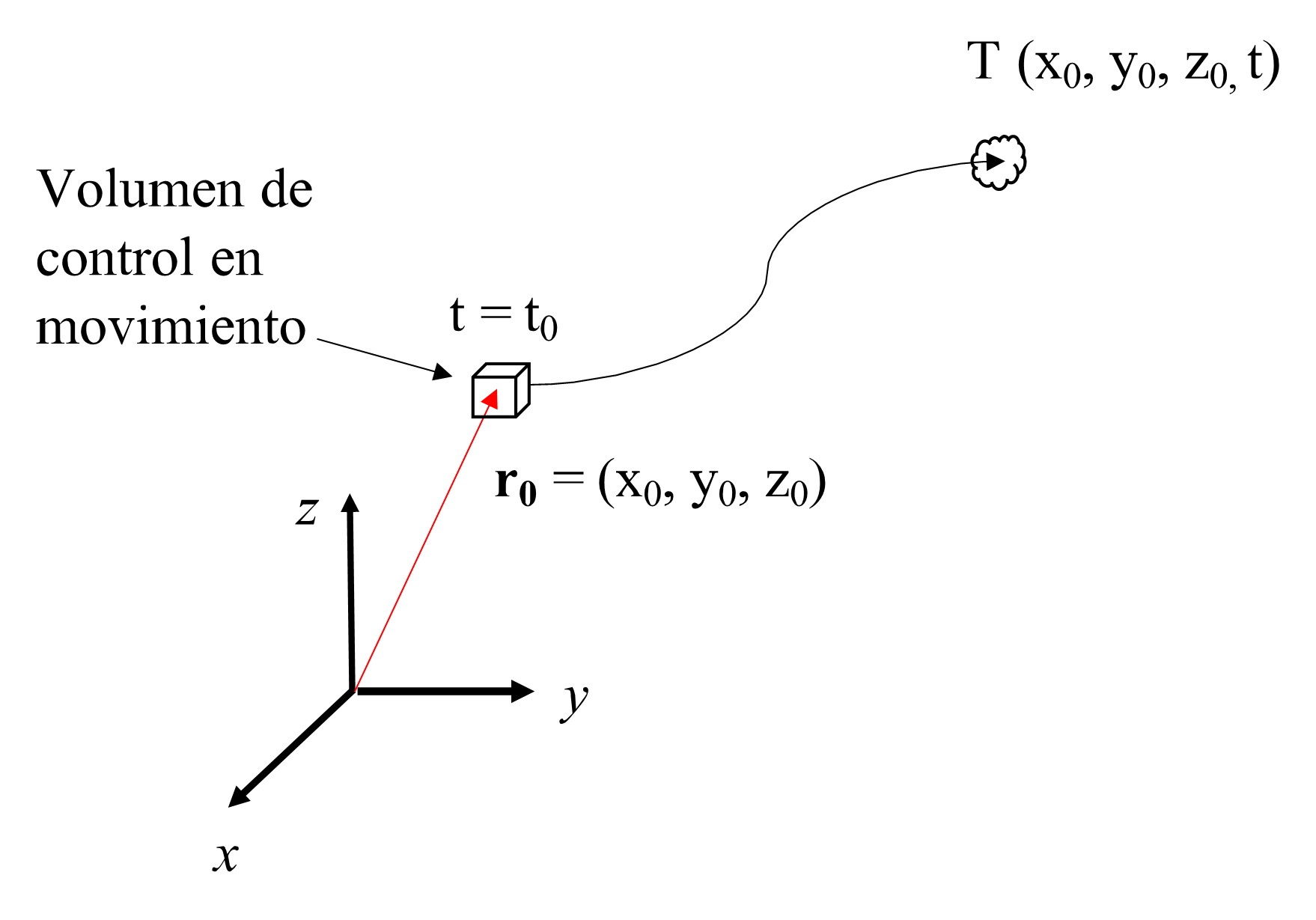
Fig. 6 Descripción Lagrangiana. Inicialmente, al tiempo \(t=t_0\), una partícula de fluido que se localiza en el punto \({\boldsymbol r}_0= \left( x_0, y_0, z_0 \right)\) tiene una cierta temperatura \(T \left( x_0, y_0, z_0, t_0 \right)\). Al transcurrir el tiempo, la partícula es arrastrada por el fluido en movimiento de modo que al tiempo \(t\) su temperatura se denota como \(T \left( x_0, y_0, z_0, t \right)\).

Descripción Euleriana

La descripción Euleriana se caracteriza por considerar volúmenes de control fijos en el espacio a través de los cuales pasan a cada instante diferentes partículas de fluido. Así, en cada punto del espacio y a cada instante las variables dependientes toman un valor único.

Esta es una descripción de campo en el sentido que se discutió previamente, es decir, una descripción que considera a todas las variables dependientes que describen al fluido como funciones de la posición y del tiempo. Por ejemplo, consideremos un fluido en movimiento que atraviesa un volumen de control esférico, el cual se encuentra fijo respecto a un cierto sistema de coordenadas (ver Fig. 7). Si elegimos un punto caracterizado por el vector de posición \({\boldsymbol r} = \left( x, y, z \right)\) dentro del volumen de control, podemos denotar la temperatura del fluido en dicho punto a un cierto instante \(t\) como \(T \left( x,y,z,t \right)\). Evidentemente, al mismo instante la temperatura puede variar en un punto vecino pero su valor es único para cada punto del espacio y a cada instante. Así como asignamos un valor a la temperatura podemos igualmente asignar valores a la densidad, \(\rho \left(x,y,z,t \right)\), la velocidad, \({\boldsymbol u} \left( x,y,z,t \right)\), y la presión, \(p \left( x,y,z,t \right)\), del fluido. En la descripción Euleriana las variables independientes son la posición y el tiempo.

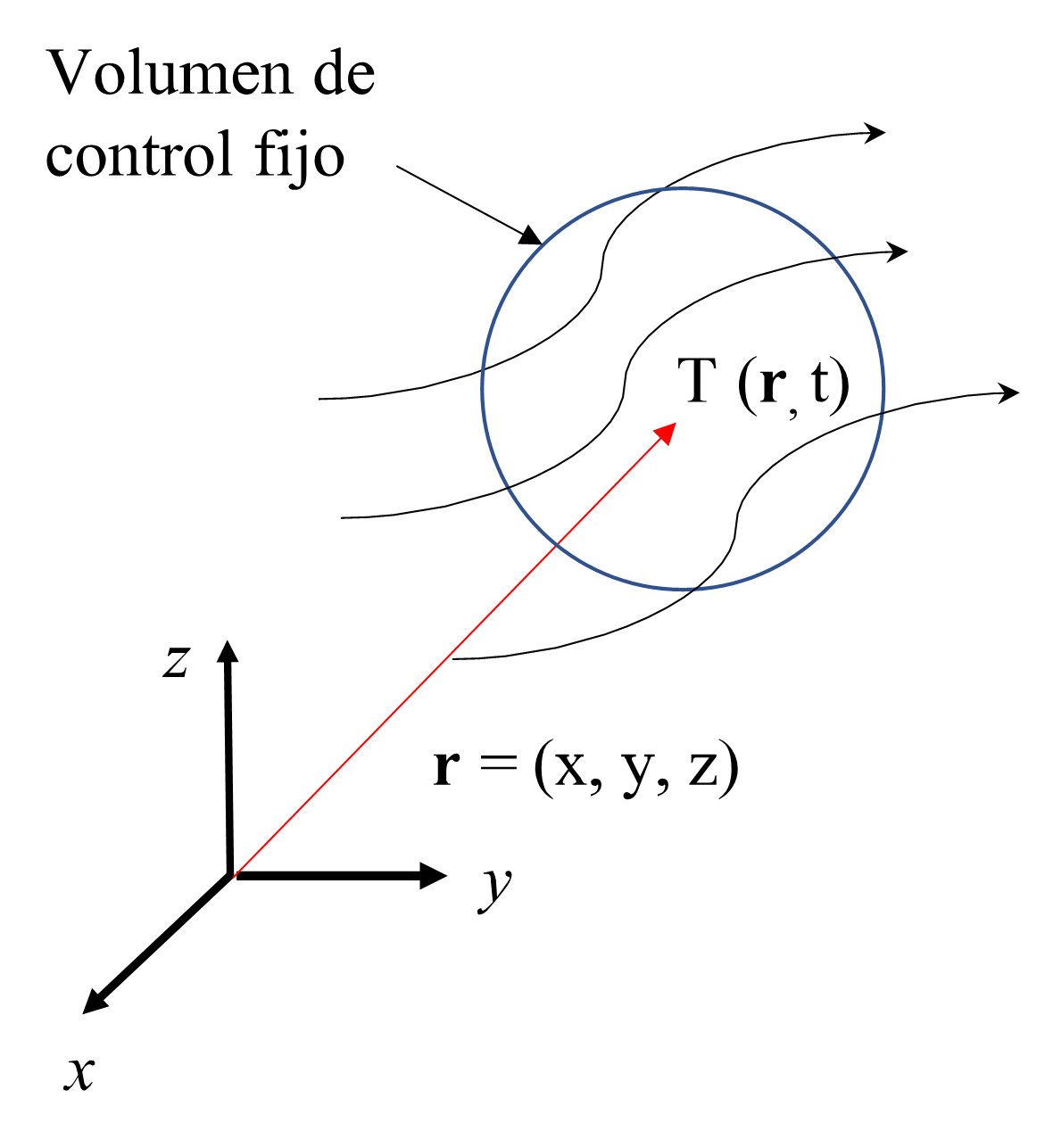
Fig. 7 Descripción Euleriana. El fluido pasa a través de un volumen de control fijo en el espacio y en cada punto \({\boldsymbol r}=\left( x,y,z \right)\) y a cada instante, \(t\), la temperatura toma un cierto valor único \(T \left( x,y,z,t \right)\).

Equivalencia de las descripciones

Debemos enfatizar que ambas descripciones son totalmente equivalentes y solo es un asunto de conveniencia el elegir una u otra. En general, la descripción Euleriana es más ampliamente utilizada en la resolución de problemas ya que es más fácil de implementar, aunque en algunas situaciones particulares, como por ejemplo la recopilación de datos atmosféricos u oceanográficos mediante globos o boyas, la descripción Lagrangiana resulta más conveniente. La dificultad principal de implementar la descripción Lagrangiana en la mecánica de fluidos es el número infinito de partículas que deberíamos perseguir para lograr una descripción amplia del flujo.

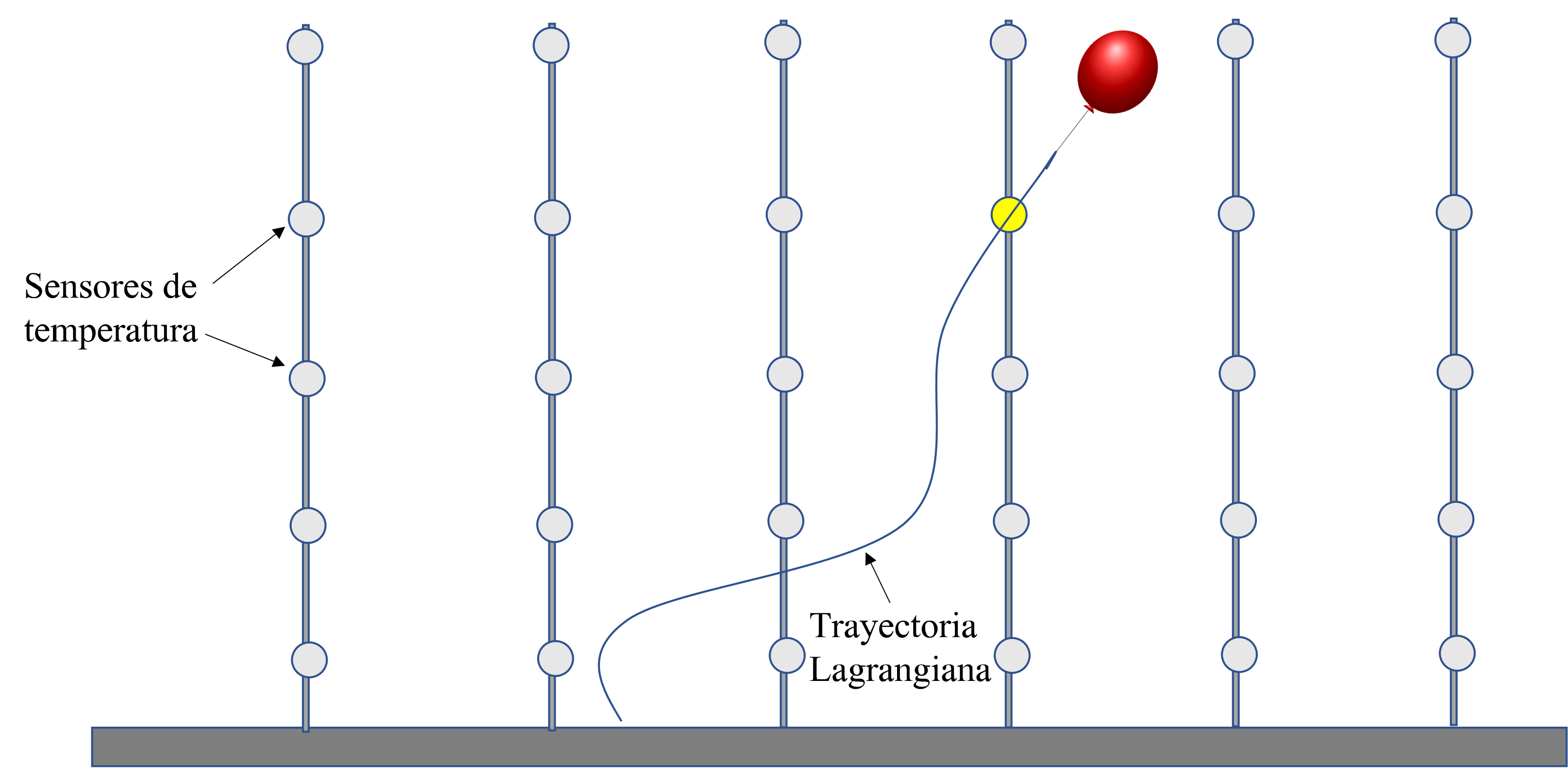
Fig. 8 Equivalencia entre las descripciones Euleriana y Lagrangiana. Los sensores de temperatura fijos en los postes permiten obtener un registro Euleriano de la temperatura. El sensor transportado por el globo ofrece un registro Lagrangiano de la temperatura. En el instante en que ambos se encuentran en el mismo punto (mostrado en amarillo), los registros coinciden.

La equivalencia entre las dos descripciones se puede ilustrar de manera sencilla (un tanto idealizada) de la siguiente manera. Supongamos que queremos caracterizar la temperatura del aire a distintas alturas conforme transcurre el tiempo en una cierta región bien delimitada, para lo cual disponemos de una serie de postes muy altos con sensores de temperatura colocados en distintos puntos a lo largo de ellos. De esta forma, tenemos la posiblidad de medir la temperatura del aire en dichos puntos fijos a lo largo del tiempo lo que nos permitiría obtener un campo Euleriano (discreto) de temperatura. Supongamos además, que contamos con globos con sensores de temperatura integrados que pueden soltarse desde la superficie de manera que registren la temperatura del aire a lo largo de la trayectoria conforme ascienden y se desplazan arrastrados por el viento. De esta manera obtendríamos un registro Lagrangiano de la temperatura. Ahora imaginemos que en algún instante el sensor de temperatura integrado a un globo se encuentra justamente en un punto donde se localiza un sensor de termperatura fijo a un poste. Evidentemente, en dicho instante ambos sensores registrarán la misma temperatura, haciendo patente la coincidencia de las descripciones Euleriana y Lagrangiana. (Ver Fig. 8)