Líneas de flujo

En la descripción del movimiento de los fluidos resulta de gran relevancia la visualización de los flujos ya sea mediante técnicas experimentales, o bien, a través de soluciones analíticas o numéricas de las ecuaciones de movimiento. Las líneas de flujo ofrecen una forma de visualizar los flujos e interpretarlos físicamente. A continuación presentaremos tres líneas de flujo, a saber, las líneas de corriente, las líneas de trayectoria y las líneas de traza, las cuales son distintas para cualquier campo de velocidades que dependa del tiempo.

Líneas de corriente

Estas líneas son fundamentales para la descripción Euleriana y se definen como aquéllas líneas cuyas tangentes en cada punto coinciden con el vector velocidad en cualquier instante. Si consideramos un campo de velocidades, \({\boldsymbol u} =(u,v,w)\), y un elemento infinitesimal de una línea de corriente, \(d{\boldsymbol r} = \left( dx,dy,dz \right)\), la ecuación que define a las líneas de corriente es:

\[{\boldsymbol u} \times d{\boldsymbol r}={\boldsymbol 0},\]

ya que en cualquier punto los vectores \({\boldsymbol u}\) y \(d{\boldsymbol r}\) son paralelos. Explícitamente podemos escribir la ecuación anterior de manera compacta:

(12)\[\frac{dx}{u}=\frac{dy}{v}=\frac{dz}{w}.\]

Notemos que estas ecuaciones se pueden expresar en la forma:

\[\begin{split}\frac{dy}{dx}&=\frac{v}{u}, \nonumber \\ \frac{dz}{dy}&=\frac{w}{v},\nonumber \\ \frac{dz}{dx}&=\frac{w}{u}, \nonumber \end{split}\]

donde se muestra que las pendientes de las líneas proyectadas en los planos \(xy\), \(yz\) y \(xz\), respectivamente, coinciden con la pendiente del vector velocidad, como indica la definición, proyectado en cada plano. La integración de las ecuaciones (12) considerando \(t\) fijo da por resultado una ecuación de la forma \(z=z \left( x,y \right)\) que representa a la línea de corriente para ese instante particular. En las líneas de corriente el tiempo es un parámetro que describe su evolución. Nótese que las líneas de corriente no se pueden cruzar (excepto en un punto de estancamiento) ya que esto implicaría que en un punto e instante dados la velocidad del fluido podría tomar dos valores diferentes.

Ilustremos la obtención de las líneas de corriente con un ejemplo sencillo. Consideremos el campo de velocidades bidimensional dado por las siguientes componentes escritas en forma adimensional:

(13)\[u = \frac{x}{1+t}, \;\;\;\;v=y, \;\;\;\;w=0,\]

de modo que las ecuaciones de las líneas de corriente son:

\[\frac{dx}{u} = \frac{dy}{v}\]

es decir,

\[(1+t) \frac{dx}{x} = \frac{dy}{y} \]

Al integrar considerando \(t\) fijo obtenemos:

\[x^{1+t} = C y, \]

donde \(C\) es una constante de integración. Para determinarla debemos dar una condición inicial lo que determinará una línea de corriente específica. Por ejemplo, si queremos la línea de corriente que pasa por el punto \(\left( x_0, y_0 \right)\) al tiempo \(t=0\), encontramos:

\[x_0 = C y_0 \;\;\;\; \Rightarrow \;\;\;\; C=\frac{x_0}{y_0}\]

por lo que la línea de corriente es:

\[y = \frac{y_0}{x_0} x^{1+t} \]

En particular, en el tiempo \(t=0\) tenemos:

\[y = \frac{y_0}{x_0} x. \]

Líneas de trayectoria

Las líneas de trayectoria son las líneas que trazan las partículas individuales en su movimiento y son fundamentales para la descripción Lagrangiana de los fluidos. Para obtener las ecuaciones que las describen hacemos uso del concepto de partícula pasiva definido previamente, ya que se desea describir la trayectoria de una partícula de esa clase inmersa en el flujo. Dado que una partícula pasiva ajusta instantáneamente su velocidad a la velocidad del flujo ambiente, podemos escribir que la velocidad de la partícula es siempre igual a la velocidad del fluido, es decir,

(14)\[{\boldsymbol u}_{particula} = {\boldsymbol u}_{fluido}.\]

La ecuación anterior es la definición formal de la advección pasiva [6]. La velocidad de la partícula está dada por la razón de cambio de su posición,

\[{\boldsymbol u}_{particula} = \left( \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right),\]

donde \(\left( x,y,z \right)\) es el vector de posición de la partícula. A su vez, la velocidad del fluido se obtiene teóricamente resolviendo las ecuaciones de movimiento, o bien, mediante mediciones experimentales, como función de las coordenadas y del tiempo:

\[{\boldsymbol u}_{fluido} = \left[ u \left( x,y,z,t \right), u \left( x,y,z,t \right), u \left( x,y,z,t \right) \right] , \]

es decir, la velocidad del fluido está dada como un campo vectorial. La condición (14) de que la velocidad de la partícula es igual a la velocidad del fluido establece las ecuaciones de las líneas de trayectoria:

(15)\[\frac{dx}{dt} = u \left( x,y,z,t \right), \]

(16)\[\frac{dy}{dt} = v \left( x,y,z,t \right), \]

(17)\[\frac{dz}{dt} = w \left( x,y,z,t \right). \]

Estas ecuaciones se conocen también como las ecuaciones de advección y son de fundamental importancia en la descripción de flujos caóticos [6].

Calculemos ahora la línea de trayectoria utilizando el mismo campo de velocidades (13). De la ecuación (15) tenemos

\[\frac{dx}{dt} = \frac{x}{1+t} \;\;\;\; \Rightarrow \;\;\;\; \frac{dx}{x} = \frac{dt}{1+t}, \]

por lo que al integrar obtenemos:

\[x = A \left( 1+t \right), \]

donde \(A\) es una constante de integración. De la ecuación (16) obtenemos:

\[\frac{dy}{dt} = y \;\;\;\; \Rightarrow \;\;\;\; \frac{dy}{y} = dt,\]

e integrando

\[y = B e^t, \]

donde \(B\) es otra constante de integración. Para determinar las constantes debemos imponer una condición inicial, por ejemplo, especificamos la línea de trayectoria que pasa por el punto \(\left( x_0,y_0 \right)\) en \(t=0\), de donde

\[A= x_0, \;\;\;\; B= y_0, \]

de modo que las coordenadas de la partícula como función de la posición inicial y del tiempo son:

\[x = x_0 \left( 1+t \right), \]

\[y = y_0 e^t. \]

También puede expresarse en términos del vector de posición de la partícula, es decir,

\[{\boldsymbol r} = \left[ x \left( x_0,t \right), y \left( y_0,t \right) \right] = \left[ x_0 \left( 1+t \right), y_0 e^t \right]. \]

Si despejamos \(t\) de la ecuación para la coordenada \(x\)

\[t= \frac{x}{x_0} -1, \]

y sustituimos en la coordenada \(y\) obtenemos

\[y = y_0 e^{\frac{x}{x_0} - 1} \]

donde observamos que no coincide con la línea de corriente.

Líneas de traza

Una línea de traza, también conocida como línea de emisión, se obtiene al inyectar de manera continua un fluido marcador en un campo de flujo en un punto determinado. Las partículas del fluido marcador actúan como partículas pasivas, moviéndose de acuerdo con lo que dicta el flujo en el que se encuentran inmersas, como ocurre cuando se introduce humo en un flujo de aire, o bien, tinta en un flujo de agua (Un ejemplo desafortunado de una línea de traza a escala geofísica puede observarse en los derrames petroleros). Una partícula de un fluido marcador que al tiempo \(t\) se encuentra en el punto \(\left( x,y,z \right)\), tuvo que haber pasado por el punto de inyección \(\left( x_0, y_0, z_0 \right)\) en un tiempo previo \(t=\tau\), es decir, la línea de traza consiste de todas las partículas que han pasado por un punto dado a un cierto tiempo previo \(\tau\). Por tanto, puede determinarse resolviendo las ecuaciones para las líneas de trayectoria Eq.(15)- Eq.(17) sujetas a la condición inicial \(x=x_0\), \(y=y_0\) y \(z=z_0\) cuando \(t=\tau\). Así, \(\tau\) actúa como un parámetro que al tomar todos los valores posibles \(\tau \le t\), define la posición instantánea de la línea de traza.

Obtengamos una línea de traza para el campo de velocidades que se utilizó previamente para ilustrar las líneas de corriente y trayectoria. Tenemos entonces

\[\frac{dx}{dt} = \frac{x}{1+t} \;\;\;\; \Rightarrow \;\;\;\; x = A \left( 1+t \right), \]

\[\frac{dy}{dt} = y \;\;\;\; \Rightarrow \;\;\;\; y = B e^t, \]

pero ahora las constantes \(A\) y \(B\) deben determinarse con la condición de frontera:

\[x=x_0, \;\;\; y=y_0, \;\;\; {\rm en} \;\; t=\tau, \]

de modo que

\[A= \frac{x_0}{1+\tau}, \;\;\; B=y_0 e^{\tau}, \]

de donde

\[x= x_0 \frac{1+t}{1+\tau}, \;\;\; y=y_0 \; e^{t- \tau}. \]

Si consideramos la línea de traza en \(t=0\) encontramos

\[x= \frac{x_0}{1+\tau}, \;\;\; y=y_0 \; e^{- \tau}, \]

donde podemos eliminar \(\tau\) despejando de la primera ecuación y sustituyendo en la segunda, es decir,

\[y= y_0 \; e^{1-x_0/x}. \]

La Fig. 14 muestra las líneas de corriente, trayectoria y traza para el campo de velocidades (13) considerando la misma condición inicial. Notemos que las líneas de corriente, trayectoria y traza no coinciden, lo que se debe al hecho de que el campo de velocidades es dependiente del tiempo.

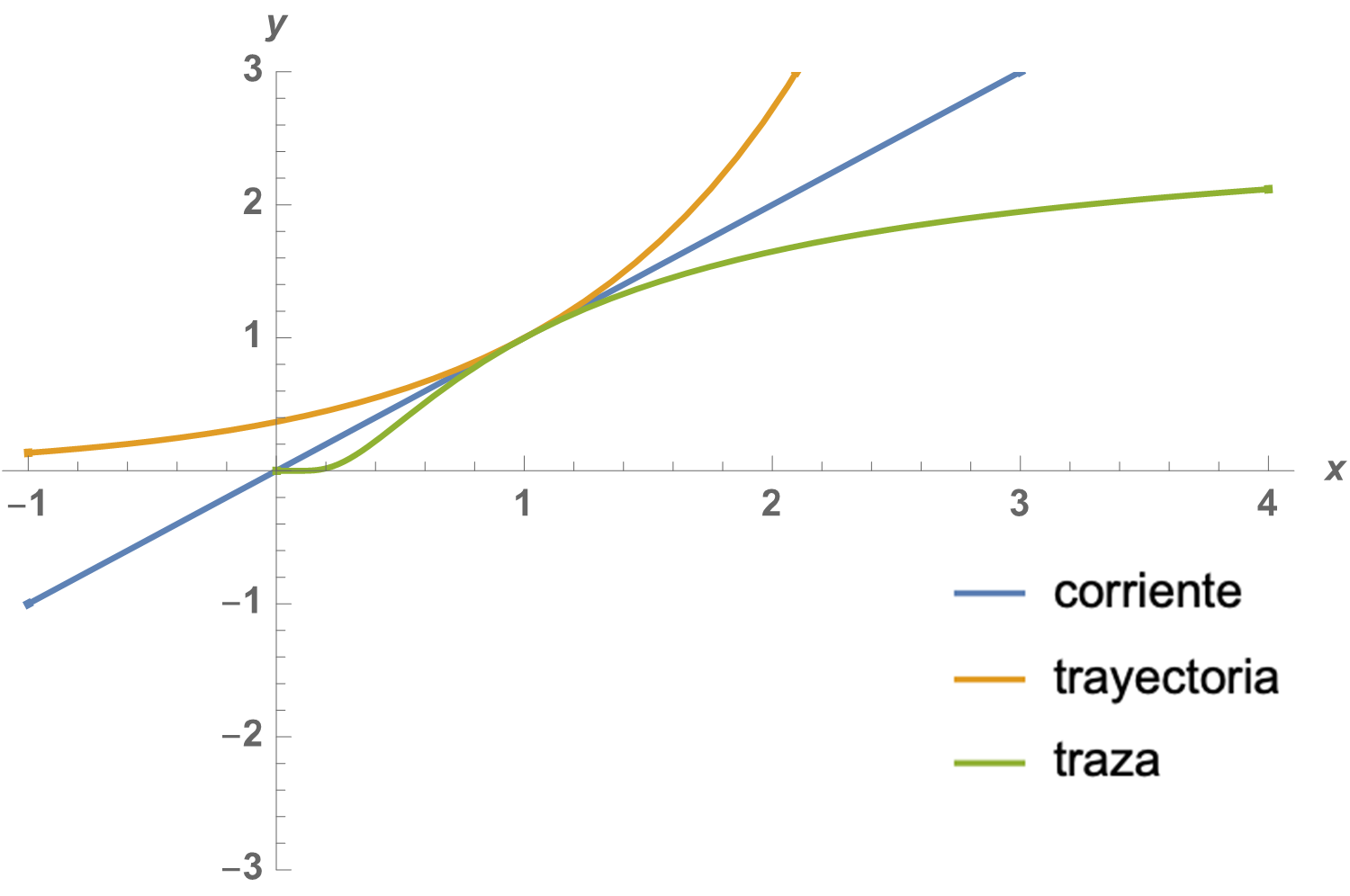
Fig. 14 Líneas de corriente, trayectoria y traza que pasan por el punto (1,1) para el tiempo \(t=0\), considerando el campo de velocidades (13)

Campo de velocidades independiente del tiempo

Veamos ahora el caso de un campo de velocidades independiente del tiempo, por ejemplo, el flujo en rotación de cuerpo rígido que analizamos previamente, dado por

\[{\boldsymbol u} = (\Omega y, -\Omega x,0).\]

Las líneas de corriente se obtienen de la ecuación:

\[\frac{dx}{u} = \frac{dy}{v} \;\;\; \Rightarrow \;\;\; \frac{dx}{\Omega y}=- \frac{dy}{\Omega x}\]

entonces,

\[x\; dx = - y\;dy \;\;\; \Rightarrow \;\;\; x^2 + y^2 =2C,\]

donde vemos que las líneas de corriente son círculos centrados en el origen con radio \(\sqrt{2C}\). La constante de integración \(C\) se puede determinar eligiendo la línea de corriente que pasa por \((x_0,y_0)\), es decir \(2C= x_0^2 + y_0^2\).

Por su parte, las líneas de trayectoria se obtienen de las ecuaciones

\[\frac{dx}{dt} = \Omega y, \]

\[\frac{dy}{dt} = -\Omega x. \]

Si derivamos la primera ecuación y substituímos la segunda

\[\frac{d^2x}{dt^2} = \Omega \frac{dy}{dt}=-\Omega^2 x, \]

que es la ecuación del oscilador armónico cuya solución es

\[x(t) = C_1 \cos \Omega t + C_2 {\rm sen} \Omega t.\]

Sustituyendo en la segunda ecuación

\[\frac{dy}{dt} = -\Omega x = -C_1 \cos \Omega t - C_2 {\rm sen} \Omega t\]

e integrando

\[y(t) = -C_1 {\rm sen} \Omega t + C_2 \cos \Omega t.\]

Si escogemos la línea de trayectoria que pasa por \(\left( x_0,y_0 \right)\) en \(t=0\) encontramos \(C_1=x_0\), \(C_2=y_0\), entonces

\[x(t) = x_0 \cos \Omega t + y_0 {\rm sen} \Omega t.\]

\[y(t) = -x_0 {\rm sen} \Omega t + y_0 \cos \Omega t.\]

de modo que:

\[x^2 + y^2 =x_0^2+y_0^2, \]

es decir, las líneas de trayectoria también son cícrulos centrados en el origen por lo que coinciden con las líneas de corriente.