Aceleración de un cuerpo rígido en líquidos

Una de las complicaciones inherentes en la descripción del movimiento de los fluidos es que a diferencia de los sólidos, su aceleración puede cambiar de un punto a otro. Sin embargo, existen situaciones particulares en las que un líquido se mueve de manera semejante a un cuerpo rígido, es decir, manteniendo un movimiento relativo nulo entre sus partículas de modo que no existen esfuerzos viscosos en el fluido. En tal caso, aunque el líquido se encuentra muy lejos del reposo, es posible analizar el flujo de manera similar al caso hidrostático. Tales situaciones se presentan, por ejemplo, cuando un recipiente que contiene un líquido se acelera uniformemente en una trayectoria rectilínea, o bien cuando un recipiente cilíndrico con un líquido en su interior rota de manera uniforme. En ambos casos, el fluido permanece estático con respecto al contenedor.

Analicemos primero el caso de un líquido dentro de un contenedor que se mueve con una aceleración constante. Si el contenedor parte del reposo, el líquido experimentará inicialmente un estado transitorio con un movimiento irregular hasta alcanzar un movimiento de cuerpo rígido con aceleración constante \(a\). Ya que en tal condición no existen esfuerzos viscosos, el movimiento está gobernado por la ecuación de Euler:

(141)\[\rho a=-\nabla p+\rho g\]

que puede expresarse como

(142)\[\nabla\rho=\rho\left(g-a\right)\]

La ecuacion (142) tiene la forma de la ecuación general de la hidrostática (70) pero con una aceleración neta que es la suma de la gravedad \(\mathbf{g}=(0, 0, −g)\) y la aceleración impuesta \(a=(ax, ay, az)\). Escribiendo la ecuación en componentes, tenemos

(143)\[\frac{\partial p}{\partial x}=-\rho a_{x}\]

(144)\[\frac{\partial p}{\partial y}=-\rho a_{y}\]

(145)\[\frac{\partial p}{\partial z}=-\rho\left(g+a_{z}\right)\]

Si el fluido se encuentra en reposo o bien se mueve a velocidad constante, las ecuaciones anteriores se reducen a las ecuaciones de la hidrostática, donde la variación de la presión se da únicamente en la dirección vertical.

Supongamos ahora que el recipiente con el fluido cae libremente debido a la gravedad. En tal caso, tenemos \(a_{x}=a_{y}=0\) y \(a_{z}=−g\), de manera que la variación de la presión respecto a las tres coordenadas es cero, o en otras palabras la presión se mantiene constante. Respecto al sistema de referencia que se mueve junto con el fluido, esta situación equivale a encontrarse en un ambiente con gravedad cero.

Si por el contrario aceleramos el fluido verticalmente con \(a_{z}=+g\), el gradiente de presión en dirección z se incrementa a \(\partial p/\partial z=-2\rho g\) por lo que la presión dentro del fluido a una altura dada será el doble de la que sería en reposo.

Consideremos ahora al caso de un contenedor con un líquido en su interior, por ejemplo una pipa, que originalmente se encuentra en reposo, como lo muestra la Fig. 53. Posteriormente, el contenedor se mueve horizontalmente hacia la derecha hasta alcanzar una aceleración constante \(a_{x}\), mientras que las aceleraciones en las direcciones \(y\) y \(z\) son cero. Debido a la inercia, el líquido se desplaza hacia la parte izquierda del contenedor modificando la forma de la superficie libre (ver Fig. 54). Evidentemente, el volumen de líquido se conserva antes y después del movimiento. En tal caso,

Fig. 53 a) Contenedor con un líquido en reposo.

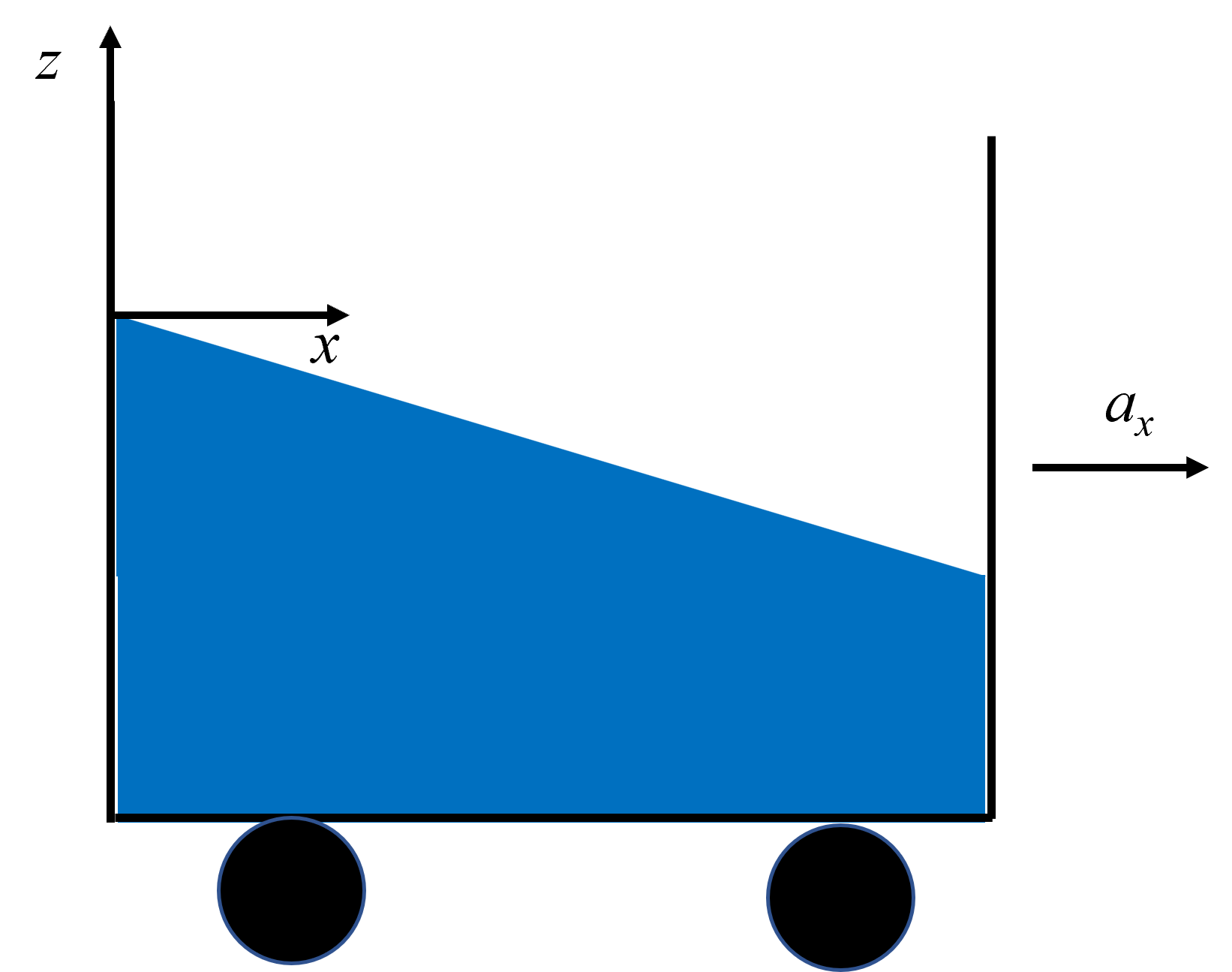
Fig. 54 b) Contenedor con un líquido con una aceleración constante a_{x} hacia la derecha.

las componentes de la ecuación (142) son

(146)\[\frac{\partial p}{\partial x}=-\rho a_{x}\]

(147)\[\frac{\partial p}{\partial y}=0\]

(148)\[\frac{\partial p}{\partial z}=-\rho g\]

La diferencial de la presión es entonces

(149)\[dp=\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial z}dz\]

(150)\[=-pa_{x}dx-\rho gdz\]

e integrando obtenemos

(151)\[p\left(x,z\right)=-\rho\left(a_{x}x+gz\right)+C\]

donde la constante de integración \(C\) debe ser determinada. Si disponemos el origen del sistema coordenado en la esquina superior izquierda del recipiente donde el líquido alcanza su mayor altura (ver Fig. 54), tenemos que en el punto \(x=0\), \(z=0\), la presión debe coincidir con la presión atmósférica, de manera que \(C=p_{atm}\), es decir,

(152)\[p\left(x,z\right)=p_{atm}-\rho\left(a_{x}x+gz\right)\]

A partir de esta expresión podemos encontrar la ecuación que determina la forma de la superficie libre. Imponiendo la condición de que sobre dicha superficie la presión es la atmosférica, \(p(x, z)=p_{atm}\), tenemos

(153)\[z=-\frac{a_{x}}{g}x\]

es decir, la superficie libre es una recta con pendiente \(−a_{x}/g\). Además, la ecuación (150) nos permite determinar las superficies de presión constante dentro del fluido, es decir, las isobaras. Haciendo \(d_{p}=0\) encontramos

(154)\[\frac{dz}{dx}=-\frac{a_{x}}{g}\]

es decir, las isobaras son líneas rectas paralelas a la superficie libre.

Analicemos ahora el problema de un líquido dentro de un contenedor cilíndrico de radio \(R\) que rota alrededor de su eje de simetría con una velocidad angular constante \(\varOmega\). Si colocamos el sistema coordenado en el fondo del recipiente alineado con dicho eje, el nivel del líquido cuando el contenedor se encuentra en reposo es \(z_0\), mientras que al alcanzar la rotación de cuerpo rígido, el líquido forma un menisco con el punto más bajo en el centro a una altura \(z_{min}\) y el punto más alto a una altura \(z_{max}\) sobre las paredes del contenedor, como lo muestra la Fig. 55. El objetivo es encontrar cómo varía la presión dentro del líquido por lo que hacemos uso de la ecuación de Euler debido a la ausencia de esfuerzos viscosos:

(155)\[\rho\left[\frac{\partial u}{\partial t}+\left(u\cdot\nabla\right)u\right]=-\nabla p+\rho g\]

y dado que el flujo es estacionario, las componentes de dicha ecuación en coordenadas Cartesianas tienen la forma

\[\begin{split}\rho\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial x}\right)&=-\frac{\partial p}{\partial x}\\ \rho\left(u\frac{\partial u}{\partial x}+ v\frac{\partial u}{\partial x}\right)&=-\frac{\partial p}{\partial x}\\ 0&=-\frac{\partial p}{\partial x}-\rho g\\\end{split}\]

Fig. 55 Contenedor rígido en rotación uniforme con velocidad angular Ω con un fluido en su interior. .

Por otra parte, las componentes del campo de velocidades del líquido en rotación de cuerpo rígido están dadas por

(156)\[u=-\varOmega y, v=\varOmega x \]

por lo que al sustituirlas en las ecuaciones anteriores obtenemos

(157)\[\frac{dp}{dx}=\rho\varOmega^{2}x \]

(158)\[\frac{dp}{dx}=\rho\varOmega^{2}y \]

(159)\[\frac{dp}{dz}=\rho g \]

Podemos entonces utilizar estas expresiones para calcular la diferencial de la presión, es decir

(160)\[dp=\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial y}dy+\frac{\partial p}{\partial z}dz \]

(161)\[=\rho\varOmega^{2}xdx+\rho\varOmega^{2}ydy-\rho gdz\]

Integrando esta ecuación, obtenemos

(162)\[p\left(x,y,z\right)=\frac{\rho\varOmega^{2}}{2}\left(x^{2}+y^{2}\right)-\rho gz+C\]

donde debemos imponer una condición de frontera para determinar la constante \(C\). Ya que sobre la superficie libre la presión coincide con la atmosférica (\(p=p_{atm}\)), lo más sencillo es evaluar en el punto central del menisco, es decir, \(x=0\), \(y=0\), \(z=z_{min}\), de manera que \(C=p_{atm}+ρgz_{min}\). Por lo tanto, la presión en cualquier punto del fluido está dada por

(163)\[p\left(x,y,z\right)=p_{atm}+\frac{\rho\varOmega^{2}}{2}\left(x^{2}+y^{2}\right)-\rho g\left(z-z_{min}\right)\]

Debido a la geometría del problema resulta conveniente reescribir la presión en coordenadas cilíndricas, lo que se logra fácilmente notando que \(r^{2}=x^{2}+y^{2}\), es decir,

(164)\[p\left(r,z\right)=p_{atm}+\frac{\rho \varOmega^{2}}{2}r^{2}-\rho g\left(z-z_{min}\right)\]

Esta expresión nos permite calcular la forma del menisco que se crea mediante la rotación del líquido, pues justamente sobre la superficie libre la presión debe coincidir con la presión atmosférica. Imponiendo la condición \(p(r, z)=p_{atm}\) en la ecuación anterior, obtenemos

(165)\[0=\frac{\rho\varOmega^{2}}{2}r^{2}-\rho g\left(z-z_{min}\right)\]

o bien,

(166)\[z-z_{min}=\frac{\varOmega^{2}r^{2}}{2g}\]

es decir, la forma del menisco es un parabolide de revolución. Además, notando que la altura máxima del menisco se alcanza en el borde del recipiente donde \(r=R\), de la expresión anterior encontramos

(167)\[z\left(R\right)=z_{max}=z_{min}+\frac{\varOmega^{2}r^{2}}{2g}\]

Sin embargo, debemos notar que tanto \(z_{min}\) como \(z_{max}\) no son conocidas y que evidentemente dependen de la velocidad angular de rotación \(\varOmega\). Para determinarlas podemos utilizar el hecho de que el volumen del líquido es el mismo antes y después de rotar. Antes de la rotación el volumen del líquido es

(168)\[V_{A}=\pi R^{2}z_{0}\]

mientras que después de la rotación podemos calcular el volumen mediante la integral

(169)\[V_{D}=\int_{0}^{2\pi}\int_{0}^{R}z\left(r\right)rdrd\theta\]

donde \(z(r)\) denota la altura del fluido como función del radio, la cual está dada por la ecuación (166), es decir,

(170)\[V_{D}=\int_{0}^{2\pi}\int_{0}^{R}\left(z_{min}+\frac{\varOmega^{2}r^{2}}{2g}\right)rdrd\theta\]

Efectuando la integral encontramos

(171)\[V_{D}=\pi R^{2}z_{min}+\frac{\pi}{g}\frac{\varOmega^{2}R^{4}}{4}=\pi R^{2}\left(z_{min}+\frac{\varOmega^{2}R^{2}}{4g}\right)\]

por lo que al igualar ambos volúmenes, tenemos

(172)\[\pi R^{2}z_{0}=\pi R^{2}\left(z_{min}+\frac{\varOmega^{2}R^{2}}{4g}\right)\]

de donde

(173)\[z_{min}=z_{0}-\frac{\varOmega^{2}R^{2}}{4g}\]

Sustituyendo en la ecuación (167), encontramos

(174)\[z_{min}=z_{0}+\frac{\varOmega^{2}R^{2}}{4g}\]

A partir de estas ecuaciones podemos determinar la diferencia de alturas entre el centro del menisco y el punto de elevación máxima del líquido, esto es

(175)\[\triangle z=z_{max}-z_{min}=\frac{\varOmega^{2}R^{2}}{2g}\]

A su vez, sustituyendo el valor de \(z_{min}\) en la ecuación (164), encontramos que en cualquier punto del fluido, la presión está dada por

(176)\[p\left(r,z\right)=p_{atm}+\frac{\rho\varOmega^{2}}{2}\left(r^{2}-\frac{R^{2}}{2}\right)-\rho g\left(z-z_{0}\right)\]

Esta ecuación muestra que para cualquier posición radial fija, la presión varía hidrostáticamente con la altura de la columna de líquido, mientras que a una altura \(z\) dada, la presión varía cuadráticamente con el radio y aumenta desde el eje del cilindro hacia las paredes del mismo. Finalmente, podemos encontrar cuáles son la superficies de presión constante en el fluido, es decir las isobaras. Si expresamos la diferencial de la presión en coordenadas cilíndricas tenemos

(177)\[dp=\rho\Omega^{2}rdr-\rho gdz\]

e imponemos la condición \(dp=0\), se tiene

(179)\[dz\mid_{p=cte}=\frac{\varOmega^{2}}{g}rdr\]

de donde al integrar obtenemos

(179)\[z\mid_{p=cte}=z_{i}=\frac{\varOmega^{2}r^{2}}{2g}+C_{i}\]

Es decir, al igual que la superficie libre las isobaras dentro del fluido son parabolides de revolución, donde la constante \(C_{i}\) es distinta para cada isobara.