Flujo en tuberías#

El flujo en tuberías es de gran relevancia práctica debido a su aplicación en instalaciones hidráulicas. En este tipo de problemas no es de interés conocer a detalle el patrón de flujo dentro de la tubería sino más bien determinar parámetros globales como por ejemplo, el gasto másico o volumétrico a la salida de una tubería, la longitud o diámetro de la tubería para una cierta aplicación o bien la potencia requerida de una bomba para abastecer un tinaco a una cierta altura. Esto puede lograrse mediante cálculos relativamente sencillos que involucran a la ecuación de Bernoulli complementada con un cúmulo de conocimientos empíricos obtenidos de la práctica constante.

Para comprender el problema que queremos atacar, analicemos primero una sitación muy sencilla. Consideremos un tinaco que almacena agua conectado a una tubería (de radio conocido) en forma de \(L\) que conduce el líquido al nivel del piso hasta la salida de la tubería, como se muestra en la Fig. 70. Supongamos que la altura de la columna de agua con respecto al piso, \(h\), no varía apreciablemente y que nos interesa conocer la velocidad media a la salida de la tubería, \(u\), o equivalentemente, el gasto volumétrico, \(Q = uA\), donde \(A\) es el área transversal del tubo. De una aplicación directa de la ecuación de Bernoulli encontramos que la velocidad media a la salida es

(366)#\[u=\sqrt{2gh}\]

donde lo único que requerimos conocer es la altura de la columna \(h\). Este resultado nos dice que si aumentamos la longitud de la tubería en cualquier cantidad, el resultado no cambia. Esto obviamente es incorrecto pues la experiencia nos dice que al incrementar la longitud de la tubería, la velocidad dismuinuirá pudiendo incluso llegar a cero para una longitud suficientemente grande. Claramente, el error se debe a que la ecuación de Bernoulli es estrictamente válida solo para fluidos ideales, es decir, en condiciones donde los efectos de fricción son completamente despreciables. Como hemos visto en los flujos estudiados en la sección anterior, un fluido viscoso se adhiere a las paredes ocasionando la aparición de esfuerzos cortantes. La existencia de una viscosidad distinta de cero y por ende de fuerzas de fricción en el flujo, dan lugar a efectos disipativos que invalidan la conservación de la energía mecánica y la ecuación de Bernoulli. Dado que la energía total se conserva, lo anterior nos indica que debido a la existencia de fricción, parte de la energía mecánica se transforma en calor que se transfiere al fluido y al medio circundante. Para efectos prácticos, la presencia de disipación en el flujo en una tubería como la mostrada en la Fig. 71, se manifiesta como una disminución efectiva de la altura de la columna de líquido, lo que ocasiona que la velocidad media a la salida sea menor que la predicha por la ecuación de Bernoulli (366). Si denominamos como \(h_f\) a la disminución de la altura de la columna debido a la presencia de disipación, podemos estimar de manera aproximada la velocidad media a la saliada de la tubería como

(367)#\[u=\sqrt{2g(h-h_{f}).}\]
../../_images/Imagen_6.6.png

Fig. 71 Flujo en una tubería en forma de L#

El problema se reduce entonces a estimar de manera adecuada la cantidad \(h_f\) . A continuación veremos que esto es posible utilizando los resultados de la sección anterior y haremos una generalización empírica que nos permite extender el ámbito de aplicacion de la ecuación de Bernoulli para realizar cálculos de flujo en tuberías.

La ecuación de Darcy y el factor de fricción#

Previamente definimos el coeficiente de fricción (ver ecuación (292) en la forma

(368)#\[C_{f}=\frac{\sigma_{zx}|_{pared}}{\rho u_{m}^{2}/2}\]

donde el esfuerzo cortante se evalúa en la pared del ducto. Para el caso del flujo de Poiseuille en un tubo de sección circular encontramos

(369)#\[\sigma_{rz}|_{pared}=-\frac{R}{2}\frac{\partial p}{\partial z}\]

donde \(R\) es el radio del tubo (ver ecuación (353). Sustituyendo en la ecuación (368) obtenemos

(370)#\[C_{f}=\frac{-\frac{R}{2}\frac{\partial p}{\partial z}}{\rho u_{m}^{2}/2}\]

que podemos expresar en la forma

(371)#\[-\frac{\partial p}{\partial z}=C_{f}\frac{\rho u_{m}^{2}}{R}\]

o bien, utilizando la ecuación (357), de manera aproximada tenemos

(372)#\[\Delta p=C_{f}\frac{L}{R}\rho u_{m}^{2}\]

La cantidad \(∆p\) se puede entender como una pérdida de energía (por unidad de volumen) en la tubería ocasionada por la fricción viscosa, es decir, debido a la existencia de disipación. Es conveniente reescribir la ecuación (372) de una manera ligeramente distinta. Para tal efecto, recordemos que la ecuación de Bernoulli se expresa como

(373)#\[p+\frac{1}{2}\rho u^{2}+\rho gz = \textrm{constante}\]

donde cada uno de los términos tiene unidades de energía por unidad de volumen. Si dividimos entre \(ρg\) tenemos

(374)#\[\frac{p}{\rho g}+\frac{1}{2}\frac{u^{2}}{g} + z = \textrm{constante}\]

donde ahora los términos de la ecuación tienen unidades de longitud. Podemos entonces reescribir la ecuación (372) en la forma

(375)#\[\frac{\Delta p}{\rho g}=C_{f}\frac{L}{R}\frac{u_{m}^{2}}{g}\]

En el cálculo de tuberías es común usar el diámetro del tubo, \(D\), en vez del radio, \(R\), y además se acostumbra introducir el factor de fricción, \(f\), en vez del coeficiente de fricción \(C_f\) , cuya relación es

(376)#\[f=4C_{f}.\]

Tomando en cuenta lo anterior, podemos expresar la ecuación (375) en la forma

(377)#\[h_f=\frac{\Delta p}{\rho g}=f\frac{L}{D}\frac{u_{m}^{2}}{2g}\]

que se conoce como la ecuación de Darcy y nos permite cuantificar, en términos de la altura de una columna de líquido, las pérdidas ocasionadas por la disipación viscosa en un tubo de longitud \(L\) y diámetro \(D\) si conocemos el factor de fricción, \(f\), y la velocidad media \(u_m\). La longitud \(h_f\) se denomina la pérdida de carga y está relacionada con la pérdida de presión en la tubería a través de la ecuación

(378)#\[\Delta p=\rho gh_{f}.\]

Aunque llegamos a la ecuación (377) partir del flujo laminar de Poiseuille, se puede aplicar también a flujos turbulentos considerando el factor de fricción adecuado, como se verá más adelante. En el caso sencillo de un flujo laminar (ver ecuación (355)), el coeficiente de fricción es \(C_f = 16/Re\), de manera que el factor de fricción queda

(379)#\[f=\frac{64}{Re} \quad (Re<2000)\]

el cual está determinado completamente al conocer el número de Reynolds

(380)#\[Re=\frac{\rho u_{m}D}{\mu}\]

En ocasiones es conveniente expresar la ecuación de Darcy (377) en términos del gasto volumétrico \(Q\) en vez de la velocidad media \(u_m\). Ya que \(Q = u_{m}A\), donde \(A\) es el área transversal del tubo de diámetro \(D\), tenemos

(381)#\[Q=u_{m}\frac{\pi D^{2}}{4}\Rightarrow u_{m}=\frac{4Q}{\pi D^{2}}\]

de donde, al sustituir en (377), encontramos

(382)#\[h_{f}=\frac{\Delta p}{\rho g}=f\frac{L}{D^{5}}\frac{8Q^{2}}{\pi^{2}g}\]

Las pérdidas de presión ocasionadas por la fricción con las paredes se conocen como pérdidas primarias pero no son las únicas que se presentan en una tubería. También existen pérdidas de presión asociadas a la presencia de accesorios como cambios de sección, válvulas, codos u obstrucciones en general, las cuales pueden estimarse a partir de consideraciones empíricas. Las pérdidas asociadas a los distintos accesorios que existen en una tubería se conocen como pérdidads secundarias. Notemos que el coeficiente \(f_L/D\) en la ecuación (377) es adimensional por lo que podemos sustituirlo por otro coeficiente adimensional \(k\) asociado a las pérdidas de presión en un aditamento particular de la tubería, por ejemplo, un codo, de manera que la pérdida de carga se puede estimar como

(383)#\[h_{f}=\frac{\Delta p}{\rho g}=f\frac{L}{D^{5}}\frac{8Q^{2}}{\pi^{2}g}\]

El coeficiente \(k\) se obtiene de manera empírica, es decir, mediante experimentación y comúnmente es proporcionado por el fabricante. Un codo a 90º tendrá un coeficiente distinto que un codo a 45º y su valor también dependerá de si el doblez está redondeado o es abrupto, entre otros factores. En el ejemplo de la Fig. 71, también existen pérdidas de presión en la conexión del tinaco con la tubería y en la salida del tubo, dependiendo del tipo de boquilla. Si llamamos \(k_i\) al coeficiente de pérdida asociado al i-ésimo aditamento, podemos estimar las pérdidas totales en la tubería en la forma

(384)#\[h_{f}=\frac{\Delta p}{\rho g}=\left(f\frac{L}{D}+\sum_{i}K_{i}\right)\frac{u_{m}^{2}}{2g}\]

Una vez cuantificadas las pérdidas, utilizaremos una ecuación de Bernoulli modificada para tomarlas en cuenta. Consideremos el ejemplo del tubo en \(L\) que se muestra en la Fig. 72 donde se indican las longitudes de los tramos de tubería y su diámetro, así como los accesorios a los que se les asocia un coeficiente de pérdida. Tomemos ahora los dos puntos mostrados para estimar la velocidad media a la salida de la tubería, es decir,

(385)#\[\frac{p_{1}}{\rho g}+\frac{u_{1}^{2}}{2g}+z_{1}=\frac{p_{2}}{\rho g}+\frac{u_{2}^{2}}{2g}+z_{2}+h_{f}\]

donde el término \(h_f\) que aparece en el lado derecho de la ecuación (385) corresponde a las pérdidas dadas por la ecuación (384). La ecuación (385) es una extensión empírica de la ecuación de Bernoulli y aunque no tiene un sustento teórico formal, su validez se verifica a partir de resultados experimentales. Como un primer caso, supongamos que el factor de fricción es conocido. Dado que los puntos 1 y 2 se encuentran expuestos al ambiente, \(p_1 = p_2 = p_{atm}\), mientras que de acuerdo al sistema de coordenadas elegido, \(z_1 = h\) y \(z_2 = 0\). Si suponemos que el diámetro del tinaco es muy grande comparado al diámetro del tubo, la columna de altura \(h\) se mantiene aproximadamente constante por lo que podemos suponer que \(u_1 ≈ 0\), de modo que la ecuación (385) se reduce a

(386)#\[h=\frac{u_{2}^{2}}{2g}+h_{f}\]

donde en este caso

(387)#\[h_{f}=\left(f\frac{\left(L_{1}+L_{2}\right)}{D}+k_{1}+k_{2}+k_{3}\right)\frac{u_{2}^{2}}{2g}\]

siendo \(L = L_1 + L_2\) la longitud total del tubo y se han sumado los coeficientes de pérdida de los accesorios. Si sustituimos (387) en (386) obtenemos

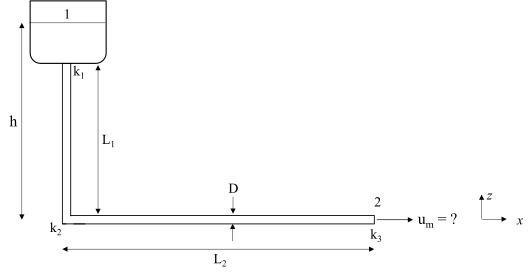
../../_images/Imagen_6.7.png

Fig. 72 Flujo en una tubería en forma de L#

(388)#\[h=\left(1+f\frac{\left(L_{1}+L_{2}\right)}{D}+k_{1}+k_{2}+k_{3}\right)\frac{u_{2}^{2}}{2g}\]

de donde la velocidad media a la salida del tubo es

(389)#\[u_{2}=\frac{2gh}{\left(1+f\frac{\left(L_{1}+L_{2}\right)}{D}+k_{1}+k_{2}+k_{3}\right)}\]

Notemos que si despreciamos las pérdidas en la ecuación anterior obtenemos el resultado ideal \(u=\sqrt{2gh}\).

Modelo simplificado de una bomba#

Consideremos un fluido incompresible donde una bomba crea una diferencia de presión \(\Delta p\) y da lugar a un gasto volumétrico \(Q\). Recordemos primero que el trabajo hecho por una fuerza \(F\) que impulsa al fluido es

(390)#\[W=F\cdot \partial x\]

donde \(dx\) es el desplazamiento. Si consideramos que la fuerza y el desplazamiento están en la misma dirección y que el desplazamiento ocasionado por la fuerza es \(\Delta x\), podemos escribir

(391)#\[W=F\Delta x\]

Recordando que \(F = \Delta p \, A\) donde \(A\) es el área transversal sobre la que se aplica la diferencia de presión \(\Delta p\), tenemos

(392)#\[W=\Delta p A \Delta x= \Delta p \Delta V\]

donde \(\Delta V\) es el volumen de fluido desplazado. Tomando la derivada temporal de la ecuación anterior tenemos

(393)#\[P_{o}=\frac{\partial W}{\partial t}=\Delta p\frac{\partial V}{\partial t}\]

y ya que \(dV/dt\) es precisamente el gasto volumétrico \(Q\), encontramos que la potencia, \(P_o\) de la bomba se puede expresar como

(394)#\[P_{o}=\Delta pQ\]

Si la eficiencia de la bomba es \(\eta\), la potencia es entonces

(395)#\[P_{o}=\frac{\Delta pQ}{\eta}\]

Dado que \(0 < \eta < 1\), si la eficiencia es baja la potencia debe incrementarse para lograr bombear al líquido. Consideremos la situación mostrada en la Fig. 73 donde ahora se coloca una bomba en el extremo bajo de la tubería de diámetro \(D\) y se desea bombear agua del punto 1 al 2 con un gasto \(Q\) determinado, por lo que se requiere conocer la potencia de la bomba necesaria para lograrlo.

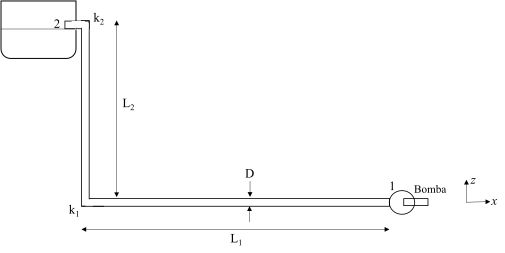
../../_images/Imagen_6.8.png

Fig. 73 Flujo en una tubería en forma de L.#

Ya que la potencia está dada por le ecuación (395) y \(Q\) es conocido, el problema se reduce a determinar \(\Delta p\). Primero, calculamos la velocidad media a lo largo de la tubería:

(396)#\[u_{m}=\frac{Q}{A}=\frac{4Q}{\pi D^{2}}\]

de donde es posible estimar el número de Reynolds

(397)#\[Re=\frac{\rho u_{m}D}{\mu}\]

Si el valor de \(Re\) es menor que 2000, podemos calcular el factor de fricción usando la fórmula laminar

(398)#\[f=\frac{64}{Re}\]

Por otro lado, si \(Re > 2000\), entonces el factor de fricción debe determinarse a partir del diagrama de Moody. De la ecuación de Bernoulli modificada tenemos

(399)#\[\frac{p_{1}}{\rho g}+\frac{u_{1}^{2}}{2g}+z_{1}=\frac{p_{2}}{\rho g}+\frac{u_{2}^{2}}{2g}+z_{2}+h_{f}\]

pero ya que la velocidad media es la misma en toda la tubería \(u_1 = u_2 = u_m\), y además \(z_1 = 0\) y \(z_2 = L_2\), obtenemos

(400)#\[\frac{p_{1}-p_{2}}{\rho g}=\frac{\Delta p}{\rho g}=L_{2}+h_{f}\]

Entonces, la diferencia de presión requerida es

(401)#\[\Delta p=\rho g(L_{2}+h_{f})\]

donde la pérdida de carga, considerando pérdidas primarias y secundarias, está dada por

(402)#\[h_{f}=\left(f\frac{\left(L_{1}+L_{2}\right)}{D}+k_{1}+k_{2}\right)\frac{u_{m}^{2}}{2g}\]

Finalmente, en términos del gasto obtenemos

(403)#\[P_{o}=\Delta pQ=\rho g(L_{2}+h_{f})Q\]
(404)#\[=\rho g\left[L_{2}+\left(f\frac{\left(L_{1}+L_{2}\right)}{D}+k_{1}+k_{2}\right)\frac{8Q^{2}}{\pi^{2}gD^{4}}\right]Q\]

Consideremos ahora la situación mostrada en la Fig. 74 en donde se desea determinar el diámetro \(D\) de la tubería de modo que el gasto volumétrico a la salida del tubo sea igual a \(Q\). Las longitudes del tubo \(L_1\), \(L_2\), \(L_3\) y \(L4\) son conocidas \((L_o = L_1 + L_2 + L_3 + L_4)\) al igual que la altura \(h\) que se supone constante, mientras que los tres codos tienen el mismo coeficiente de pérdida, \(k\). Despreciaremos las pérdidas en la unión del tubo con el tinaco y en la boquilla de salida. Supondremos que el flujo es laminar de modo que el factor de fricción está dado por \(f = 64/Re\). Estableciendo la ecuación de Bernoulli modificada (385) entre los puntos 1 y 2, y tomando en cuenta que las presiones son iguales a la atmosférica obtenemos

(405)#\[z_{1}-z_{2}=h-L_{3}=\frac{u_{2}^{2}}{2g} + h_f\]

donde hemos hecho la aproximación \(u1 ≈ 0\). Las pérdidas de carga primarias y secundarias son

(406)#\[h_{f}=\left(f\frac{L_{o}}{D} + 3k\right)\frac{u_{m}^{2}}{2g}\]

donde el factor de fricción está dado por

(407)#\[f=\frac{64}{Re}=\frac{64\mu}{\rho u_{m}D}\]

Si sustituimos (406) y (407) en (405), expresando la velocidad media en términos del gasto volumétrico, \(u_m = 4 Q /\pi D^2\), encontramos

(408)#\[h-L_{3}=\frac{1}{2g}\frac{16Q^{2}}{\pi^{2}D^{4}}\left[1+\frac{64{\mu}}{\rho\frac{4Q}{\pi D^{2}}D}\frac{L_{O}}{D}+3k\right]\]
(409)#\[=\frac{8Q^{2}}{\pi^{2}gD^{4}}\left[1+\frac{16\pi{\mu}L}{\rho Q}+3k\right]\]

Si sustituimos (6.50) y (6.51) en (6.49), expresando la velocidad media en términos del gasto volumétrico, \(u_m = 4 Q /\pi D^2\), encontramos

(410)#\[D=\left[\frac{8Q^{2}}{\pi^{2}g(h-L_{3})}\left(1+\frac{16\pi{\mu}L}{\rho Q}+3Q\right)^{\frac{1}{4}} \right]\]
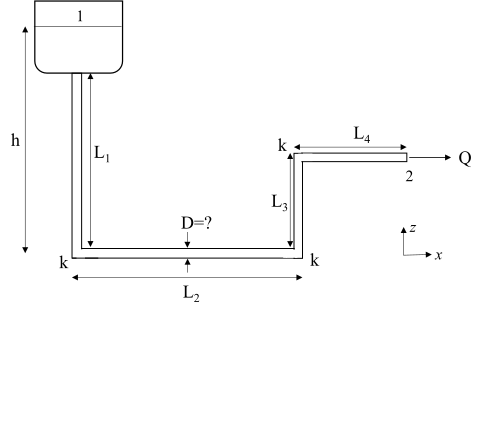
../../_images/Imagen_6.9.png

Fig. 74 Tinaco#