Mecánica de fluidos y otras áreas
Mecánica de fluidos y otras áreas#
La mecánica de fluidos tiene un lugar preponderante en el desarrollo de las energías renovables. En muchos de los procesos de generación, transferencia o almacenamiento de energía, la presencia de fluidos, ya sea en estado líquido o gaseoso, es inherente. El aprovechamiento de la energía cinética del viento a través de aerogeneradores, los calentadores solares de agua, la producción de electricidad mediante caídas de agua o la conversión de energía térmica en electricidad a través de fluidos extraídos de pozos geotérmicos, se encuentran entre las aplicaciones más comunes. Otras tecnologías como la refrigeración solar o el uso combinado de paneles fotovoltaicos y sistemas de captación del calor solar mediante fluidos con nanopartículas son menos conocidos pero igualmente importantes y en continuo desarrollo. A su vez, el interés en la energía oceánica con sus diferentes variantes tales como gradiente salino, corrientes marinas o mareomotriz se ha incrementado debido al inmenso potencial que representa el oceáno a nivel global.
La comprensión del clima en la Tierra y su posible predicción se cuentan entre los retos científicos más importantes de los últimos cien años, y en las décadas recientes esta área de la ciencia, donde la mecánica de fluidos juega un papel fundamental, ha cobrado cada vez mayor relevancia debido a los problemas que enfrentamos con el cambio climático [1]. Dichos problemas hacen más apremiante aún el desarrollo de tecnologías amigables con el ambiente que suplanten la utilización de los combustibles fósiles.
La mecánica de fluidos forma parte de la física clásica y sus fundamentos se encuentran en la mecánica Newtoniana y la termodinámica. Esta disciplina utiliza un enfoque macroscópico que considera a un fluido como un medio continuo susceptible de ser descrito por variables de campo (como la temperatura, la presión, la densidad y la velocidad) que satisfacen ciertas ecuaciones surgidas de los principios generales de conservación de masa, cantidad de movimiento y energía. Tratándose de un medio deformable que evoluciona en el tiempo, describir el movimiento de los fluidos es en general más complicado que describir el movimiento de los cuerpos sólidos. Matemáticamente la dificultad principal subyace en el hecho de que las ecuaciones que describen el movimiento de los fluidos son no lineales.
Los fenómenos estudiados por la mecánica de fluidos abarcan un rango muy amplio de escalas de longitud que van desde los flujos astrofísicos que se manifiestan en el espacio exterior, hasta el nado de bacterias en microorganismos, pasando por los que tienen lugar a escala terrestre en los ríos, la atmósfera y los océanos. Una manera de caracterizar a los distintos tipos de flujos es a través de un parámetro adimensional conocido como el número de Reynolds que se expresa de la siguiente manera:
donde \(U\) y \(L\) representan escalas de velocidad y longitud, respectivamente, características del flujo, mientras que \(\rho\) y \(\mu\) son la densidad de masa y la viscosidad del fluido, respectivamente. El número de Reynolds es el parámetro más importante en la mecánica de fluidos y a reserva de una discusión más amplia que se hará posteriormente, se puede interpretar como el cociente de dos ingredientes que actúan sobre el fluido, por un lado, la inercia entendida como la tendencia del fluido a mantener su estado de movimiento y por otro, la fuerza viscosa que manifiesta a las fuerzas de fricción en el fluido que tratan de poner fin o reducir dicho movimiento. Cuando el número de Reynolds es muy grande (\(Re \gg 1\)) la inercia del flujo domina sobre la fuerza viscosa y el flujo tiende a ser lo que llamamos turbulento, es decir, un flujo irregular (caótico) y con una estructura muy compleja. Por el contrario, cuando el número de Reynolds es pequeño (\(Re \leq 1\)) el flujo tiende a ser laminar, es decir, ordenado y con una estructura sencilla.
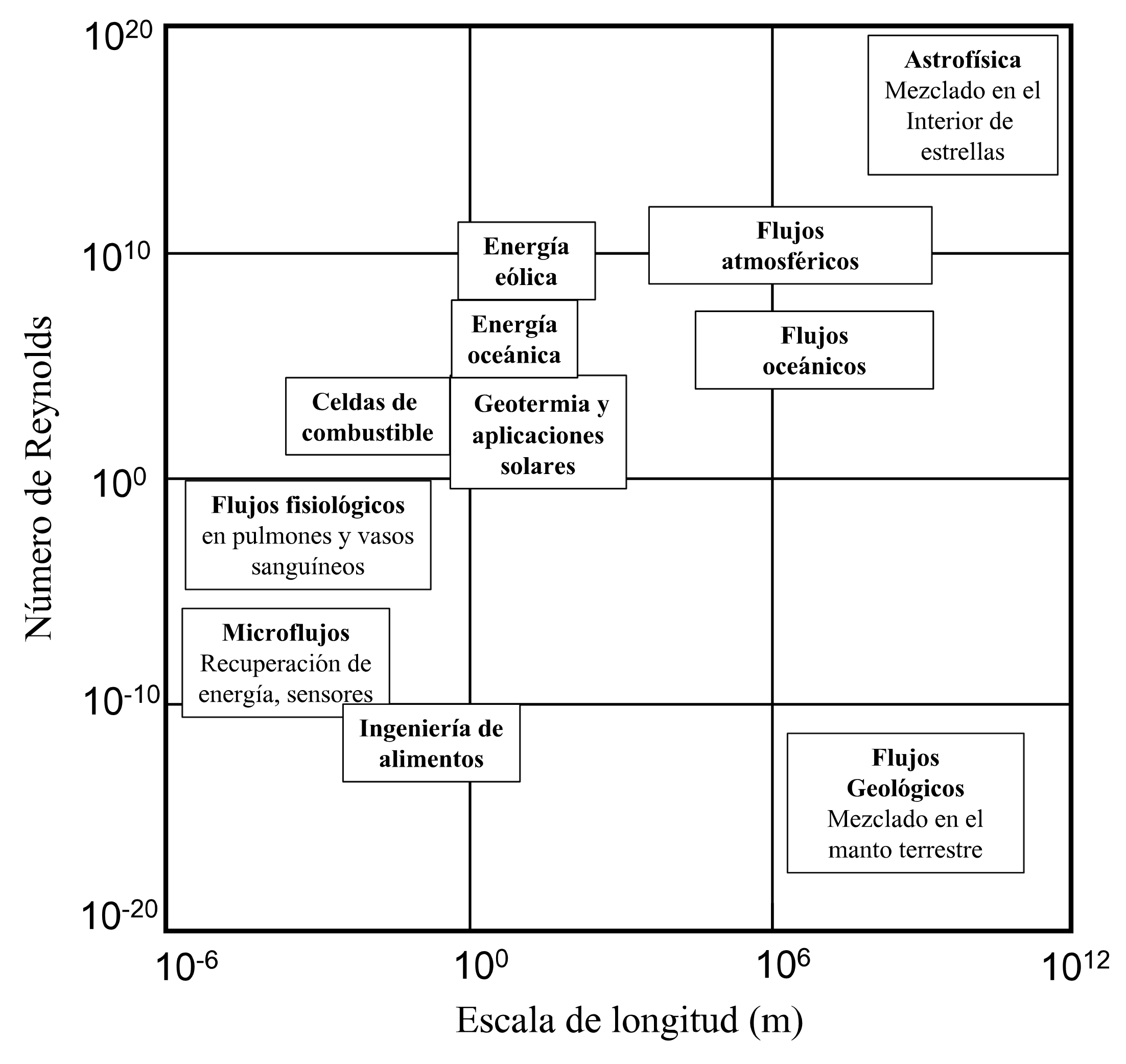
Fig. 1 Ilustración de distintas aplicaciones de la mecánica de fluidos de acuerdo al número de Reynolds de los flujos involucrados y su escala de longitud.#
En la Fig. 1 se ilustran distintos fenómenos y aplicaciones tecnológicas que involucran flujos en un rango muy amplio de números de Reynolds y escalas de longitud. Se trata de visualizar de manera aproximada la gran variedad de problemas a los que se aboca la mecánica de fluidos. Es importante mencionar que en la mayoría de los fenómenos naturales y aplicaciones tecnológicas, en particular aquellas relacionadas con el aprovechamiento de la energía, los flujos involucrados tienden a ser turbulentos.
Iniciemos con la definición de algunos conceptos importantes.
