Variación de la presión en la atmósfera
Variación de la presión en la atmósfera#
La atmósfera de la Tierra es una capa de aire extremadamente delgada (comparada con su extensión alrededor de la Tierra) que se extiende desde su superficie hasta el borde del espacio exterior, mantiéndose unida a la superficie por la gravedad. La atmósfera no es uniforme y las propiedades del aire cambian constantemente con el tiempo y la posición. Se compone de cuatro capas denominadas tropósfera, estratósfera, mesoesfera y termoesfera, siendo la primera la más cercana a la superficie de la Tierra con una extensión aproximada de 11 km, aunque su grosor puede variar dependiendo de la latitud. De hecho, en los trópicos donde la temperatura es mayor la tropósfera es más gruesa (alrededor de 16 km) mientras que en los polos es más delgada (aproximadamente 8 km). Las distintas curvas de la Fig. 46 muestran la variación de la densidad del aire, la presión, la temperatura y la velocidad del sonido como función de la altura en la atmósfera, a partir de un modelo promediado conocido com Atmósfera Estándar [8] realizado por la NASA en los años 60 del siglo XX pero que describe razonablemente bien el comportamiento de la atmósfera.
La presión en la atmósfera varía con la altura de la superficie. Sabemos que la presión al nivel del mar es mayor que la presión en la cumbre de una montaña ya que la columna de aire por encima de la superficie es mayor en el primer caso que en el segundo.
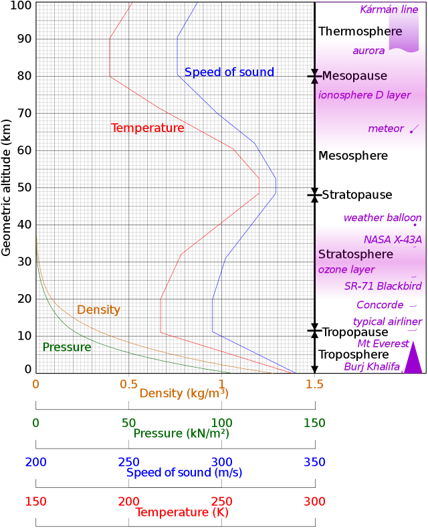
Fig. 46 La gráfica muestra resultados del modelo Atmósfera Estándar realizado por la NASA donde se compara la densidad del aire, la presión, la velocidad del sonido y la temperatura de la atmósfera a distintas alturas, mostrando el cambio de estas variables en las capas de la atmósfera. En la parte inferior se encuentran las escalas para las distintas variables [8].#
Aunque el aire de la atmósfera no es estrictamente un fluido en reposo, podemos hacer esta suposición para calcular de manera simple la variación de la presión con la altura partiendo de la ecuación de la hidrostática
Los resultados obtenidos de esta forma pueden contrastarse con datos experimentales y verificar que se aproximan a la realidad. La discusión que haremos a continuación se aplica únicamente a la tropósfera, es decir, a la capa más cercana a la superficie de la Tierra. Es posible hacer distintas aproximaciones o modelos de cómo varía la presión en esta capa de la atmósfera, siendo el más sencillo suponer que el aire es incompresible, es decir, que su densidad es constante. Si hacemos esta suposición e integramos la ecuación imponiendo la condición de que sobre la superficie \((z=0)\) la presión coincide con la presión atmosférica, obtenemos
que es la ecuación (85) que previamente encontramos, la cual nos dice que la presión disminuye linealmente con la altura. Sin embargo, suponer que la densidad del aire es constante a distintas alturas es una aproximación adecuada solo en una región muy cercana a la superficie pero es incorrecta a mayores alturas. De hecho, se sabe que la densidad del aire disminuye con la altura (ver Fig. 46) por lo que un mejor modelo es considerar que el aire es un gas ideal que cumple la ecuación de estado
donde \(R\) es la constante del gas. De esta forma la ecuación hidrostática queda
de modo que la presión está regida por la ecuación diferencial
donde \(C\) es la constante de integración. Imponiendo la condición \(p(0)=p_{atm}\), obtenemos
lo que indica que la presión disminuye exponencialmente con la altura. La suposición de que la temperatura permanece constante no es adecuada ya que realmente la temperatura más alta se encuentra cerca de la superficie y disminuye a mayores alturas, como se observa en la Fig. 46.
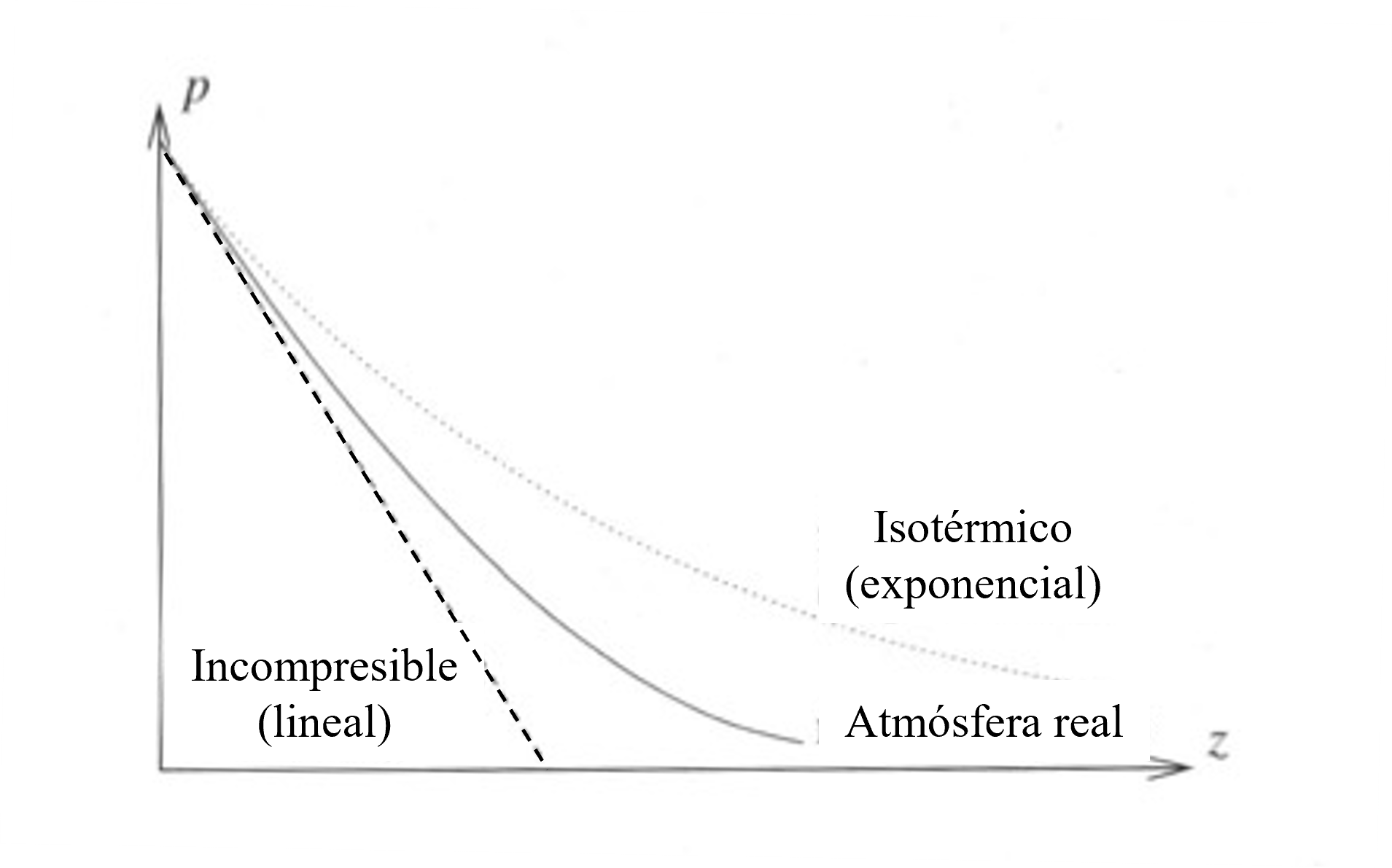
Fig. 47 Comparación de la variación de la presión de la atmósfera con la altura para distintas aproximaciones.#
Una aproximación que se acerca bastante a la realidad es suponer que la temperatura disminuye linealmente con la altura, es decir,
donde la constante \(\alpha\) se denomina lapso de temperatura y tiene un valor aproximado de \(6.5°\textrm{C/km}\). Con esta suposición, la ecuación hidrostática toma la forma
o bien
Si se integra la presión desde \(p_0\) a \(p\) y la altura de \(0\) a \(z\), es decir
tenemos que
En la Fig. 47 se muestra la comparación del comportamiento de la presión en la atmósfera para los tres modelos considerados. Observamos que el modelo más realista en donde la temperatura disminuye linealmente se encuentra entre el modelo con densidad constante (variación lineal) y el modelo que considera un gas ideal donde la temperatura se mantiene constante (variación exponencial).
