La derivada material

Veamos cómo calcular la razón de cambio temporal de cualquier variable, \(f\), relevante para la descripción de un fluido en movimiento, por ejemplo, la temperatura, la densidad o una componente de la velocidad. De acuerdo a la descripción Lagrangiana, \(f\) se puede expresar como

\[f=f(x_0,y_0,z_0,t)\]

donde \(x_0\), \(y_0\) y \(z_0\) son las coordenadas de la posición inicial de la partícula de fluido. Por su parte, utilizando la descripción Euleriana, tenemos

\[f=f(x,y,z,t)\]

donde \(x\), \(y\), \(z\) son las coordenadas de cualquier punto en el espacio. Supongamos ahora que durante un pequeño intervalo de tiempo \(\Delta t\), la variable \(f\) sufre un cambio \(\Delta f\), de modo que:

\[\Delta f = \frac{\partial f}{\partial t} \Delta t + \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y + \frac{\partial f}{\partial z} \Delta z\]

donde el lado derecho corresponde a la variación de la función \(f\) de acuerdo a la descripción Euleriana. Si dividimos por \(\Delta t\),

(3)\[\frac{\Delta f}{\Delta t} = \frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} \frac{\Delta x}{\Delta t} + \frac{\partial f}{\partial y} \frac{\Delta y}{\Delta t} + \frac{\partial f}{\partial z} \frac{\Delta z}{\Delta t},\]

y tomamos el límite cuando \(\Delta t \rightarrow 0\), del lado izquierdo de la ecuación anterior obtenemos:

\[\lim_{\Delta t \rightarrow 0} \frac{\Delta f}{\Delta t} = \frac{Df}{Dt}\]

que corresponde al cambio total de \(f\) de acuerdo a la descripción Lagrangiana. Notemos que aunque \(f\) depende de las coordenadas \(x_0\), \(y_0\) y \(z_0\), estas son constantes por lo que la única variación efectiva es la temporal. Por otra parte, si tomamos el límite del lado derecho de la ecuación (3), tenemos que:

\[\lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} = u\]

donde \(u\) es la componente de la velocidad en dirección \(x\). De manera similar, en el límite \(\Delta t \rightarrow 0\), los cocientes \(\Delta y/\Delta t\) y \(\Delta z/\Delta t\) tienden a las componentes de la velocidad \(v\) y \(w\), en las direcciones \(y\) y \(z\), respectivamente. De esta forma, la ecuación (3) se transforma en:

(4)\[\frac{Df}{D t} = \frac{\partial f}{\partial t} + u \frac{\partial f}{\partial x} + v \frac{\partial f}{\partial y} + w \frac{\partial f}{\partial z}.\]

La expresión (4) establece la equivalencia entre las descripciones Lagrangiana y Euleriana. El término \(Df/Dt\) se conoce como la \(\textit{ derivada material}\) y representa la razón de cambio total de la variable \(f\) de acuerdo a un observador que sigue a una partícula de fluido (La notación \(D/Dt\) es comúnmente utilizada en la mayoría de los textos). Por su parte, el lado derecho representa el cambio total de la variable \(f\) de acuerdo a la descripción Euleriana. Notemos que es posible expresarla en la forma

(5)\[\frac{Df}{D t} = \frac{\partial f}{\partial t} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}) f,\]

donde \({\boldsymbol u} = (u,v,w)\) es el campo de velocidades y

\[{\boldsymbol \nabla} \equiv \left( \frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z} \right)\]

es el operador diferencial Nabla. El término \(\partial f/\partial t\) representa la variación local de \(f\), ya que esta puede cambiar con el tiempo en cualquier punto del espacio. Por su parte, \(({\boldsymbol u} \cdot {\boldsymbol \nabla}) f\) representa el cambio en la variable \(f\) debido a que un cierto elemento de fluido cambia su posición con el tiempo y toma diferentes valores de \(f\) conforme fluye, es decir, este término manifiesta la presencia de convección en el fluido.

Podemos definir el operador derivada material en la forma

(6)\[\frac{D}{D t} = \frac{\partial }{\partial t} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}).\]

Nótese que se trata de un operador escalar que puede actuar sobre una función escalar como la presión, la densidad o la temperatura, o bien sobre una función vectorial, como la velocidad. En tal caso tenemos la aceleración del fluido, es decir,

(7)\[{\bf a}= \frac{D{\boldsymbol u}}{D t} = \frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}) {\boldsymbol u},\]

donde el término \(D{\boldsymbol u}/D t\) se conoce como la aceleración Lagrangiana, es decir, la aceleración de un elemento de fluido al desplazarse. Por su parte, el lado derecho de la ecuación (7) corresponde a la aceleración Euleriana que tiene dos partes, la aceleración local \(\partial {\boldsymbol u}/\partial t\) y la aceleración convectiva \(({\boldsymbol u} \cdot {\boldsymbol \nabla}) {\boldsymbol u}\) que es un término no lineal. De manera explícita tenemos

(8)\[\begin{split}\frac{\partial {\boldsymbol u}}{\partial t} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}) {\boldsymbol u} \; & = & \left[\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z}, \right. \nonumber \\ & & \;\; \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z}, \nonumber \\ & & \;\;\left. \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \right] \end{split}\]

La no linealidad de la aceleración Euleriana manifiesta que el fluido es un medio deformable en el que distintos puntos pueden tener aceleraciones diferentes.

Si utilizamos la notación \({\boldsymbol u} = (u_1,u_2,u_3)\) para el campo de velocidades y \({\boldsymbol r}=(x_1,x_2,x_3)\) para el vector de posición, podemos escribir la ecuación (4) en la forma

\[\begin{split}\frac{Df}{D t} &= \frac{\partial f}{\partial t} + u_1 \frac{\partial f}{\partial x_1} + u_2 \frac{\partial f}{\partial x_2} + u_3 \frac{\partial f}{\partial x_3}, \nonumber \\ & = \frac{\partial f}{\partial t} + \sum_{j=1}^3 u_j \frac{\partial f}{\partial x_j}, \nonumber\end{split}\]

donde podemos omitir el símbolo de sumatoria \(\sum\) acordando que el índice repetido \(j\) indica una suma desde \(j=1\) a 3, es decir

\[\frac{Df}{D t} = \frac{\partial f}{\partial t} + u_j \frac{\partial f}{\partial x_j}\]

De igual forma, podemos expresar la componente \(i\) de la aceleración como:

\[\frac{Du_i}{D t} = \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j}\]

donde el índice \(i\) se denomina \(\textit{ índice libre}\) (no repetido) y toma los valores 1, 2, 3. Por su parte, el índice repetido \(j\), que toma los mismos valores, también se denomina índice contraído. Los índices \(i\) y \(j\) se denominan índices mudos ya que podemos usar cualesquiera otras letras para denotarlos, por ejemplo, \(k\) y \(m\). Analicemos ahora las descripciones Lagrangiana y Euleriana en dos flujos sencillos.

Flujo en rotación de cuerpo rígido: vórtice forzado

Consideremos el movimiento de un fluido que rota como un cuerpo rígido con una velocidad angular constante \(\Omega\), lo que puede lograrse, por ejemplo, haciendo rotar un balde de agua. Si describimos el flujo Lagrangianamente, cada partícula de fluido describirá una trayectoria circular; si elegimos una partícula que al tiempo \(t=0\) se encuentra en la posición \(\left( x_0,0 \right)\) (ver figura Fig. 9), su trayectoria como función de tiempo puede expresarse en la forma:

(9)\[{\boldsymbol r} (x_0,t) = (x_0 \;\cos \Omega t, x_0 \;{\rm sen} \Omega t),\]

por lo que la velocidad de la partícula es:

(10)\[ {\boldsymbol u} (x_0,t) = \frac{D{\boldsymbol r}}{Dt} (x_0,t) = (-\Omega x_0 \;{\rm sen} \Omega t, \Omega x_0 \;\cos \Omega t).\]

A su vez, la aceleración de la partícula Lagrangiana toma la forma:

\[{\bf a}= \frac{D{\boldsymbol u}}{Dt} (x_0,t) = (-\Omega^2 x_0 \;\cos \Omega t, -\Omega^2 x_0 \;{\rm sen} \Omega t)\]

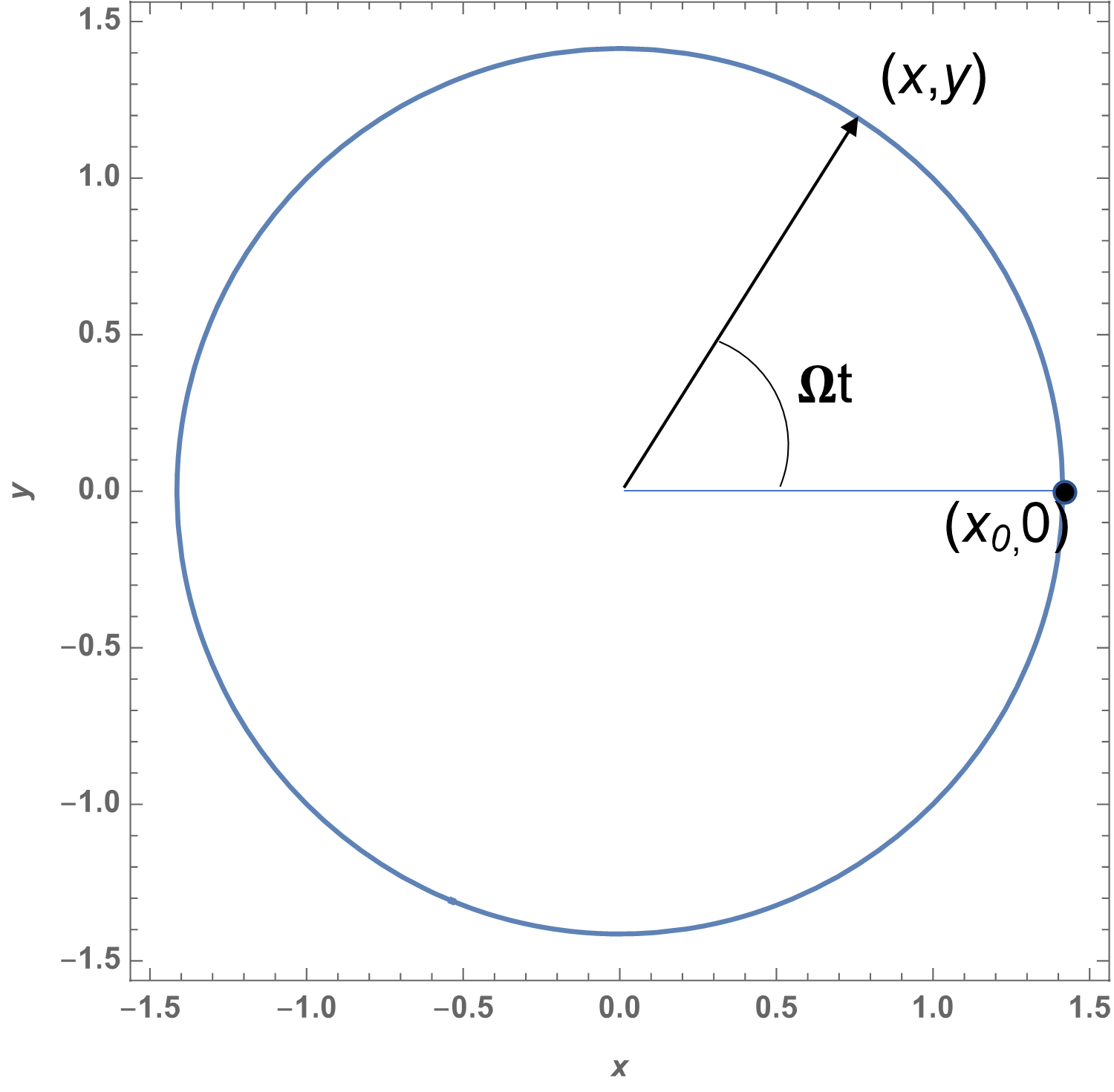
Fig. 9 Trayectoria de una partícula de fluido que se mueve en movimiento circular uniforme con velocidad angular constante \(\Omega\).

Para describir este flujo Eulerianamente, debemos visualizarlo como un campo de velocidades. Notemos que las coordenadas \((x,y)\) de cualquier punto en el fluido están dadas por:

(11)\[x = x_0 \;\cos \Omega t, \;\;\; y = x_0 \;{\rm sen} \Omega t,\]

de modo que expresando la velocidad (10) en términos de dichas coordenadas encontramos el campo Euleriano:

\[{\boldsymbol u} (x,y) = (-\Omega y, \Omega x )\]

Mientras que la velocidad Lagrangiana es una función del tiempo, Eulerianamente el campo de velocidades es independiente del tiempo. A su vez, la aceleración Euleriana toma la forma:

\[\begin{split}{\bf a} & = \cancel{\frac{\partial {\boldsymbol u}}{\partial t}} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}) {\boldsymbol u} \nonumber \\ & = \left[-\Omega y \;\frac{\partial }{\partial x} + \Omega x \;\frac{\partial }{\partial y} \right] (-\Omega y, \Omega x) \nonumber \\ & = (-\Omega^2 x, - \Omega^2 y). \nonumber\end{split}\]

Al sustituir las ecuaciones (11) en la ecuación anterior, vemos que las aceleraciones Lagrangiana y Euleriana son totalmente compatibles. Las figuras Fig. 10 y Fig. 11 muestra los campos de velocidades y aceleraciones de este flujo.

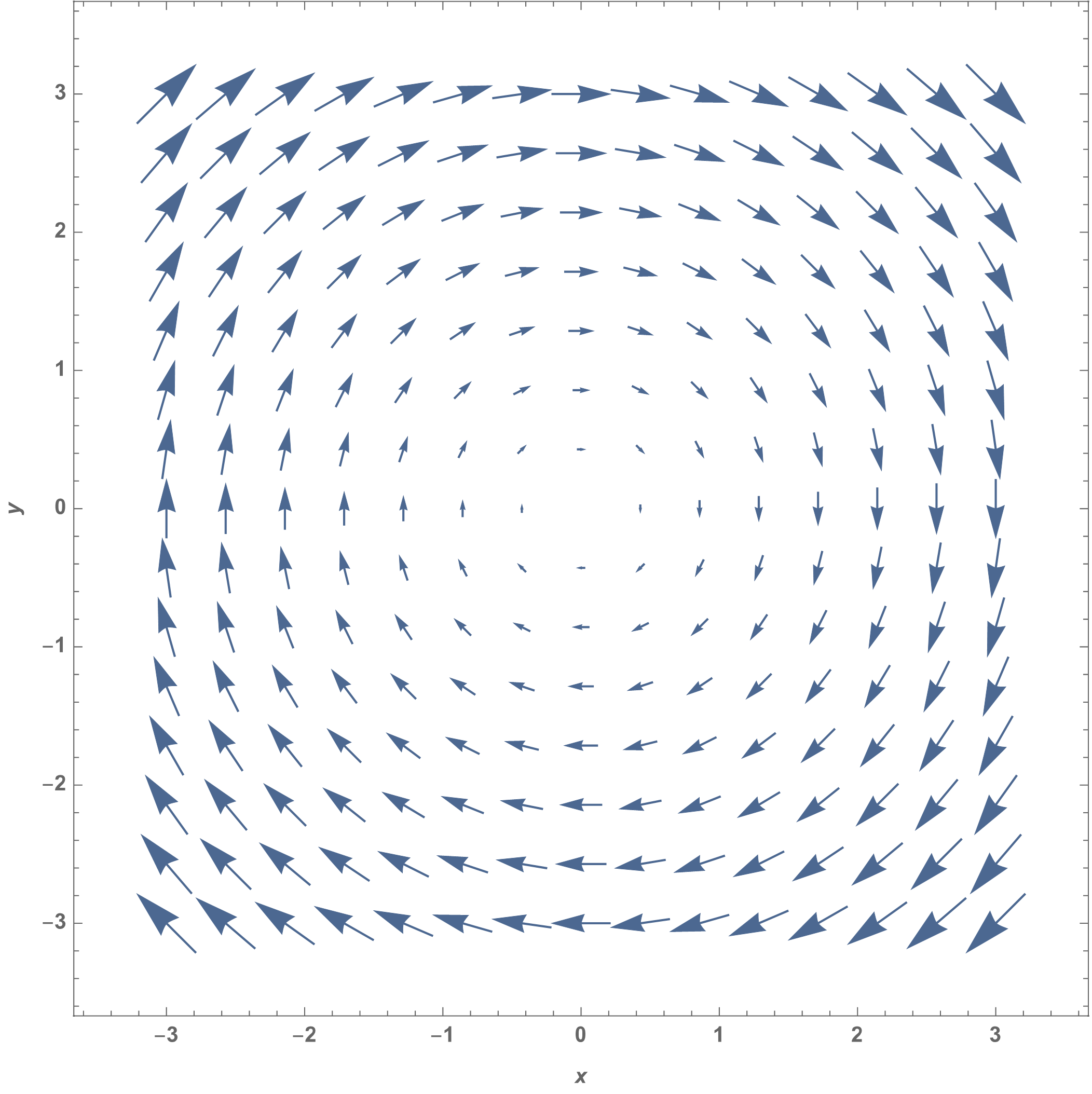
Fig. 10 Campo de velocidades de un flujo en rotación de cuerpo rígido

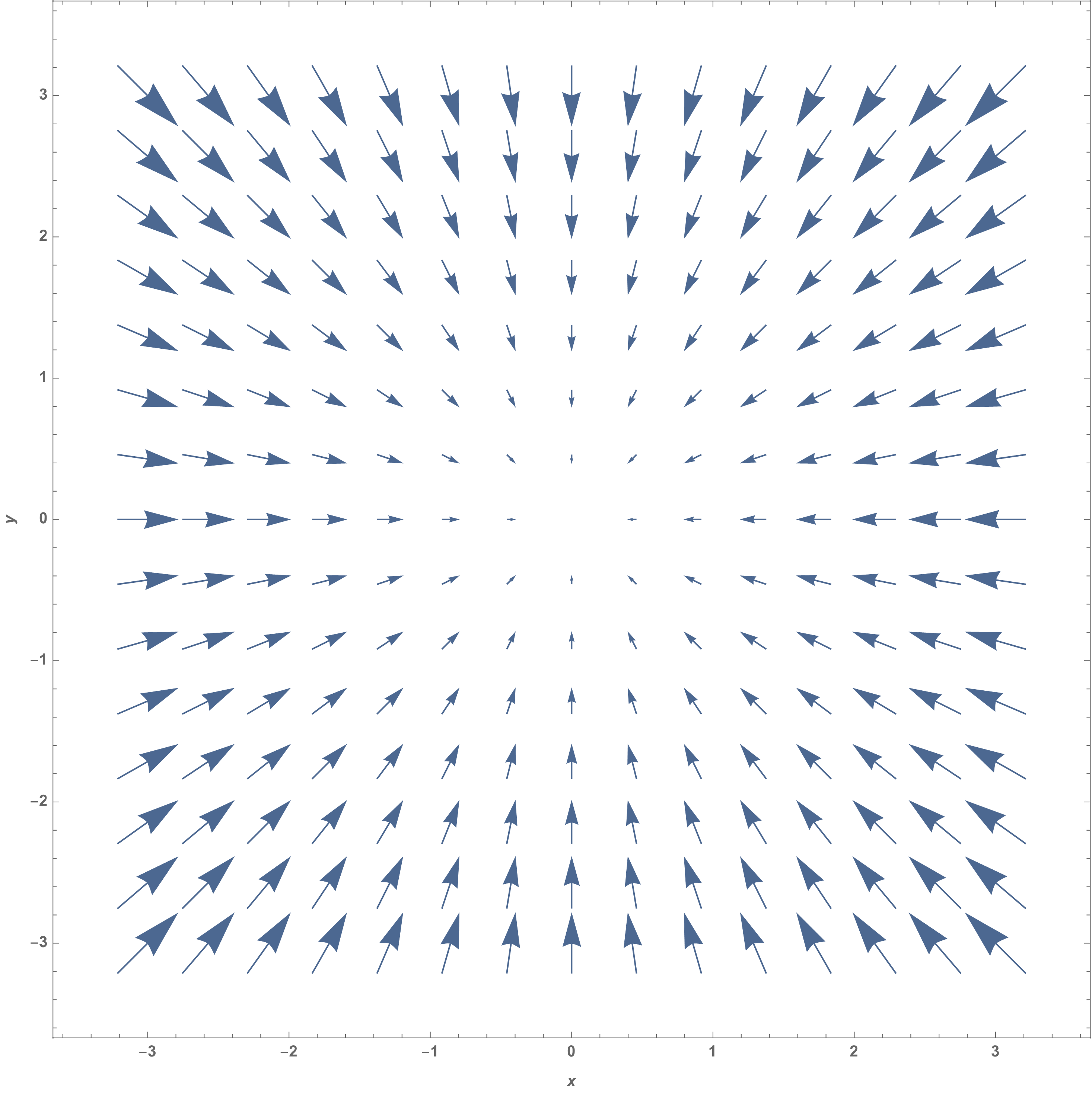
Fig. 11 campo de aceleraciones de un flujo en rotación de cuerpo rígido

Flujo con un punto de estancamiento

Ahora consideremos un flujo en donde la trayectoria Lagrangiana de una partícula de fluido está descrita por:

\[{\boldsymbol r} (x_0,y_0,z_0, t) = (x_0 \;e^{\alpha t}, y_0 \;e^{-\alpha t}, z_0) \]

donde \(\alpha\) es una constante positiva. Evaluando en \(t=0\) obtenemos la posición inicial de la partícula \((x_0,y_0,z_0)\). Al transcurrir el tiempo, el fluido es estirado en dirección \(x\) y encogido en dirección \(y\) debido a los factores \(e^{\alpha t}\) y \(e^{-\alpha t}\). La velocidad de la partícula está dada por:

\[{\boldsymbol u} (x_0,t) = \frac{D{\boldsymbol r}}{Dt} (x_0,y_0,z_0,t) = (\alpha x_0 e^{\alpha t}, -\alpha y_0 e^{-\alpha t}, 0), \]

mientras que su aceleración es:

\[{\bf a}= \frac{D{\boldsymbol u}}{Dt} (x_0,y_0,z_0,t) = (\alpha^2 x_0 e^{\alpha t}, \alpha^2 y_0 e^{-\alpha t}, 0)\]

Tanto la velocidad como la aceleración de la partícula son funciones de la posición inicial y del tiempo.

Para describir este flujo Eulerianamente, notamos que las coordenadas de la partícula son:

\[x=x_0 \;e^{\alpha t}, \;\;\; y= y_0 \;e^{-\alpha t}, \;\;\; z= z_0,\]

por lo que al sustituir en la velocidad Lagrangiana, obtenemos el campo de velocidades en la forma:

\[{\boldsymbol u} (x,y) = (\alpha x, -\alpha y, 0 )\]

Se trata de un campo estacionario donde el origen es un punto de estancamiento, es decir, un punto donde la velocidad del fluido se hace cero. La aceleración Euleriana es:

\[\begin{split}{\bf a} & = \cancel{\frac{\partial {\boldsymbol u}}{\partial t}} + ({\boldsymbol u} \cdot {\boldsymbol \nabla}) {\boldsymbol u} \nonumber \\ & = \left[\alpha x \;\frac{\partial }{\partial x} - \alpha y \;\frac{\partial }{\partial y} \right] (\alpha x, -\alpha y) \nonumber \\ & = (\alpha^2 x, \alpha^2 y) \nonumber\end{split}\]

Evidentemente, si en vez de las coordenadas \(\left( x,y \right)\) utilizamos las coordenadas de la partícula en términos de la posición inicial y el tiempo, recobramos la aceleración Lagrangiana. Las figuras Fig. 12 y Fig. 13, se muestran los campos de velocidades y aceleraciones de este flujo.

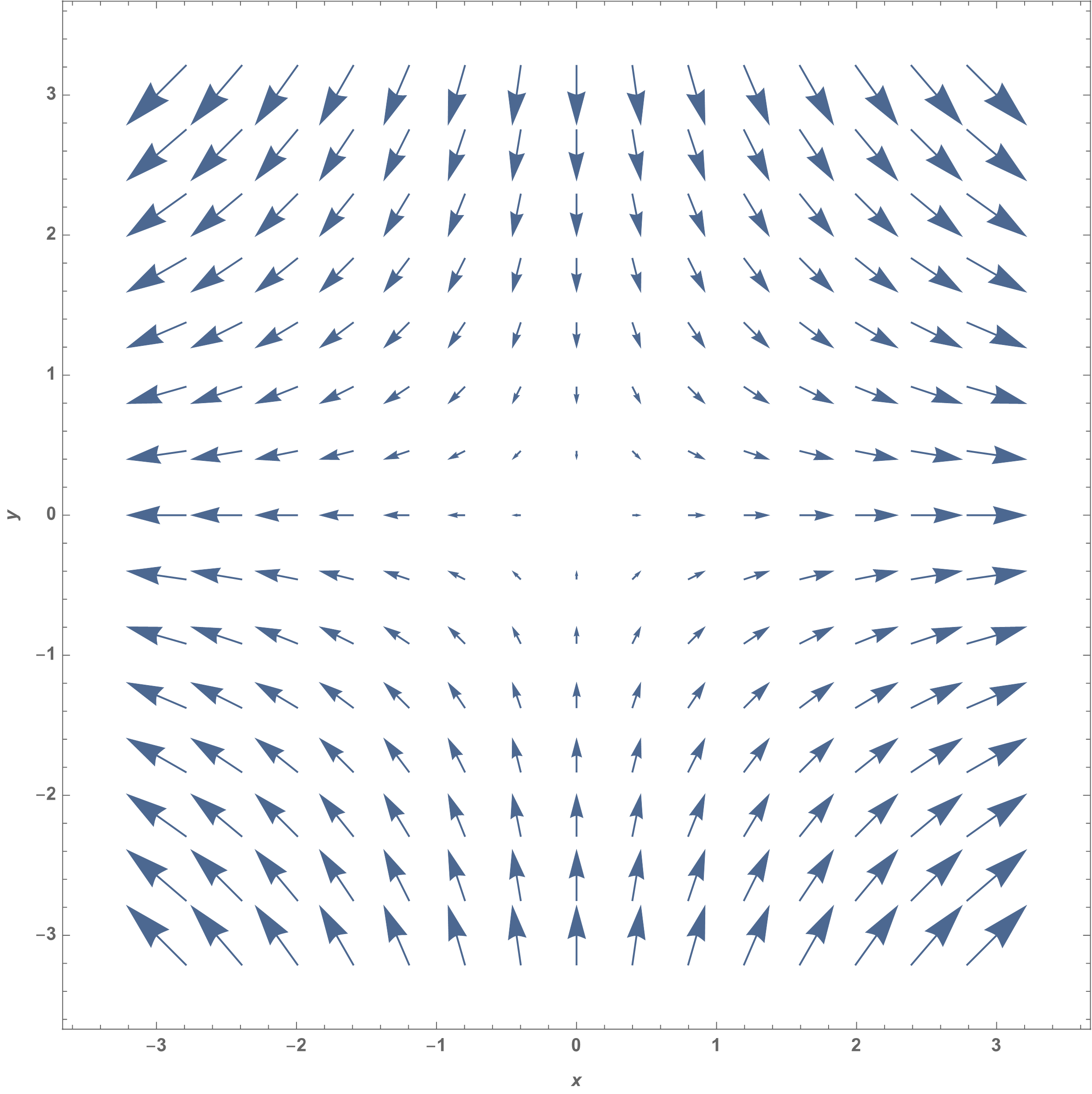
Fig. 12 Campo de velocidades de un flujo con un punto de estancamiento.

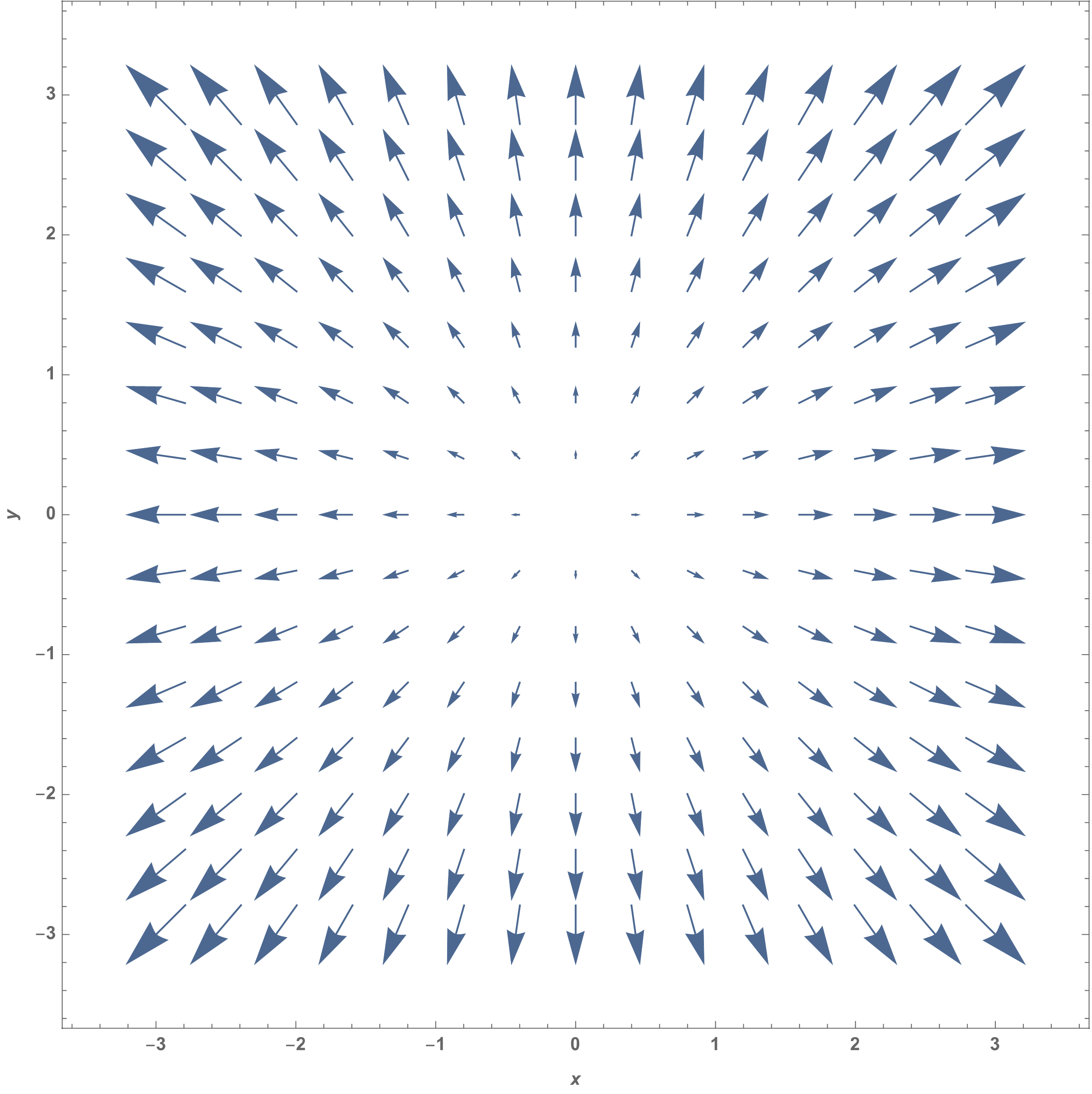
Fig. 13 campo de aceleraciones de un flujo con un punto de estancamiento.

Notemos que:

\[xy= x_0 \;e^{\alpha t} y_0 \;e^{-\alpha t}= x_0y_0={\rm cte}, \]

de modo que:

\[y =\frac{{\rm cte.}}{x}, \]

es decir, las trayectorias de las partículas son hipérbolas.