La presión en un fluido en reposo
La presión en un fluido en reposo#
Cuando el fluido está en reposo podemos demostrar que la fuerza de superficie normal por unidad de área, es decir, la presión, es igual en todas direcciones. Para tal efecto, consideremos un volumen de control dentro del fluido en reposo de forma triangular y de grosor unitario en direción normal al plano del triángulo, como se muestra en la figura Fig. 37. Sobre los catetos
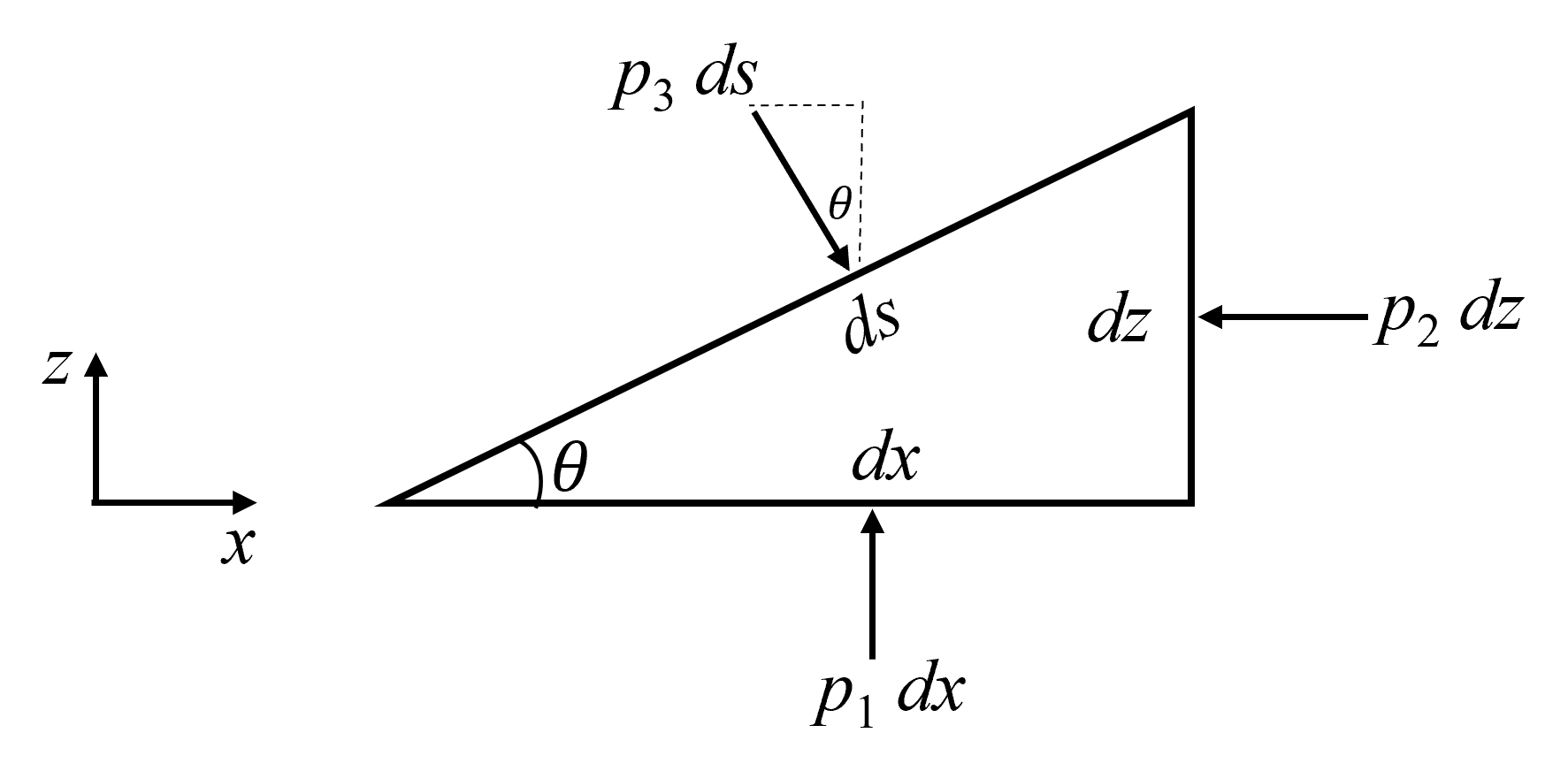
Fig. 37 Fuerzas de presión aplicadas sobre un volumen de control triangular en un fluido en reposo.#
del triángulo rectángulo \(dx\) y \(dz\) y su hipotenusa \(ds\) actúan las presiones \(p_{1}, p_{2}\) y \(p_{3}\), respectivamente. Las únicas fuerzas aplicadas sobre el elemento de fluido son las fuerzas de presión normales a las caras del triángulo y la fuerza gravitacional, es decir, el peso del elemento. Ya que no existe aceleración en dirección horizontal, si hacemos un balance de fuerzas en la dirección \(x\) considerando la componente correspondiente que actúa sobre la hipotenusa, encontramos
Pero notemos que \(dz = ds \cos \theta\), de modo que \(p_{2}=p_{3}\). Si ahora hacemos el balance de fuerzas en dirección vertical, tenemos
donde hemos incluido la fuerza gravitacional por unidad de volumen \(\left(-\rho g \right)\) multiplicada por el volumen del elemento. Ya que \(dx = ds \cos \theta\), encontramos
Si ahora hacemos tender el elemento triangular a un punto \(dz \to 0\), la gravedad desaparece y obtenemos \(p_{1}=p_{3}\). Entonces encontramos que para cualquier punto del fluido
es decir, la presión es independiente de la orientación angular de la superficie por lo que se trata de una cantidad escalar. La forma triangular del elemento de fluido considerada no es relevante, en general podemos hacer un balance de fuerzas sobre cualquier forma arbitraria y encontraremos el mismo resultado.
