La ecuación de conservación de masa

Las ecuaciones de transporte para la masa, el momento y la energía pueden establecerse de diversas formas. En un fluido en movimiento podemos considerar, de manera equivalente, un elemento de volumen determinado (volumen de control), que se desplaza junto con el fluido (descripción Lagrangiana), o bien, un volumen fijo en el espacio (descripción Euleriana). Por ejemplo, si el volumen se desplaza con el fluido, el principio de conservación de la masa establece que la masa contenida en el volumen de control se conserva, es decir, es una constante, independientemente del movimiento del fluido y de la deformación que sufra dicho volumen. Otra manera de establecer este principio es considerando un volumen de control fijo en el espacio, de modo que el fluido en movimiento pase a través de él (ver Fig. 28).

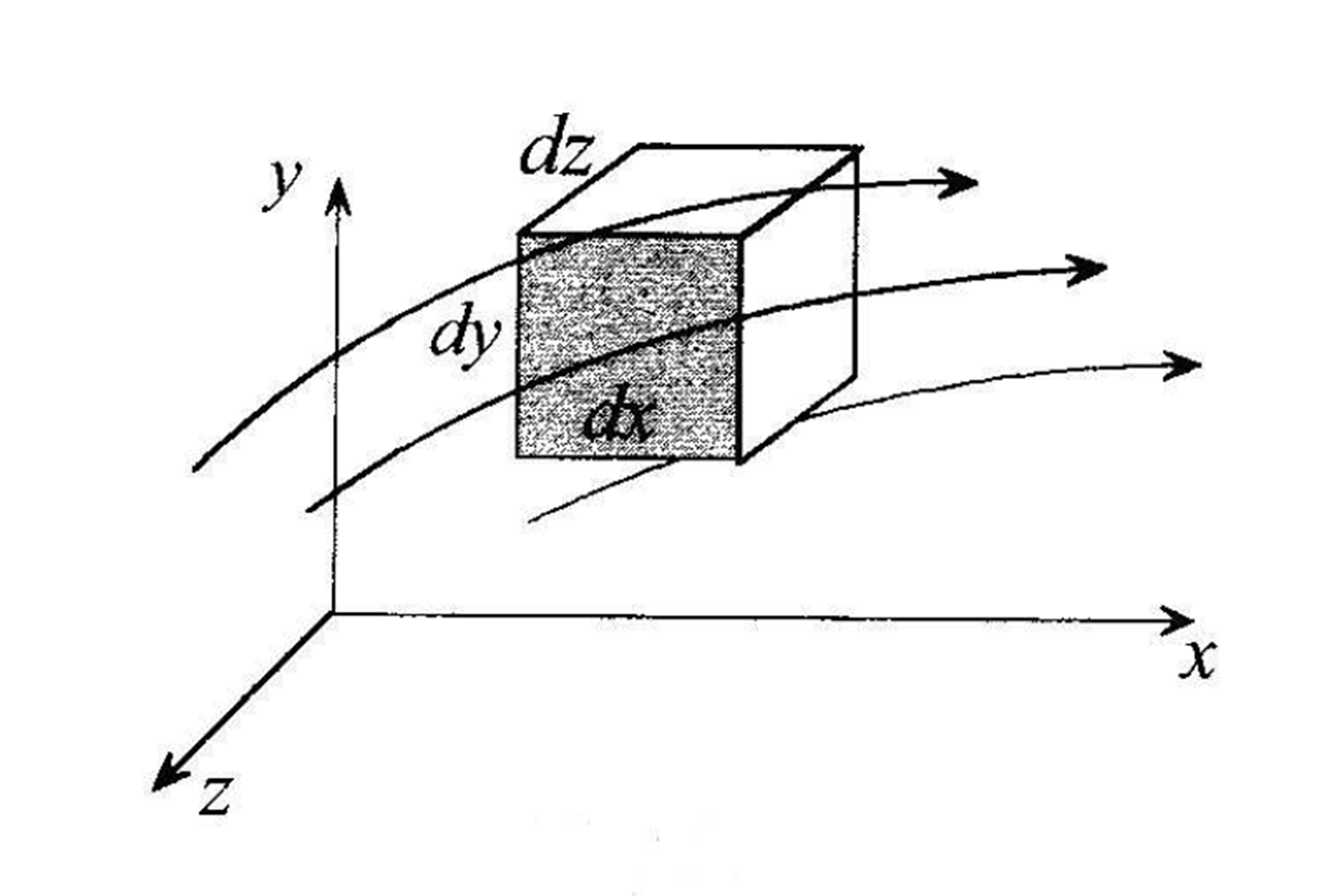
Fig. 28 Volumen de control fijo en el espacio donde existe un fluido en movimiento

Decimos entonces que el cambio temporal de la masa en el volumen de control (V. C.) es igual al flujo de masa que atraviesa sus fronteras, es decir, la masa dentro del volumen sólo puede variar por razón de que entre o salga masa a través de sus fronteras debido al movimiento del fluido:

Tasa de cambio de la masa dentro del V.C. = Tasa a la que entra masa al V.C. - Tasa a la que sale masa del V.C.

Lo que estamos estableciendo entonces es que la masa no puede crearse ni destruirse dentro del volumen de control. Para formular matemáticamente este principio, consideremos un volumen de control \((dx)(dy)(dz)\) fijo en una región de flujo, como la que aparece en la figura Fig. 29a, donde por simplicidad no se muestra la dirección \(z\).

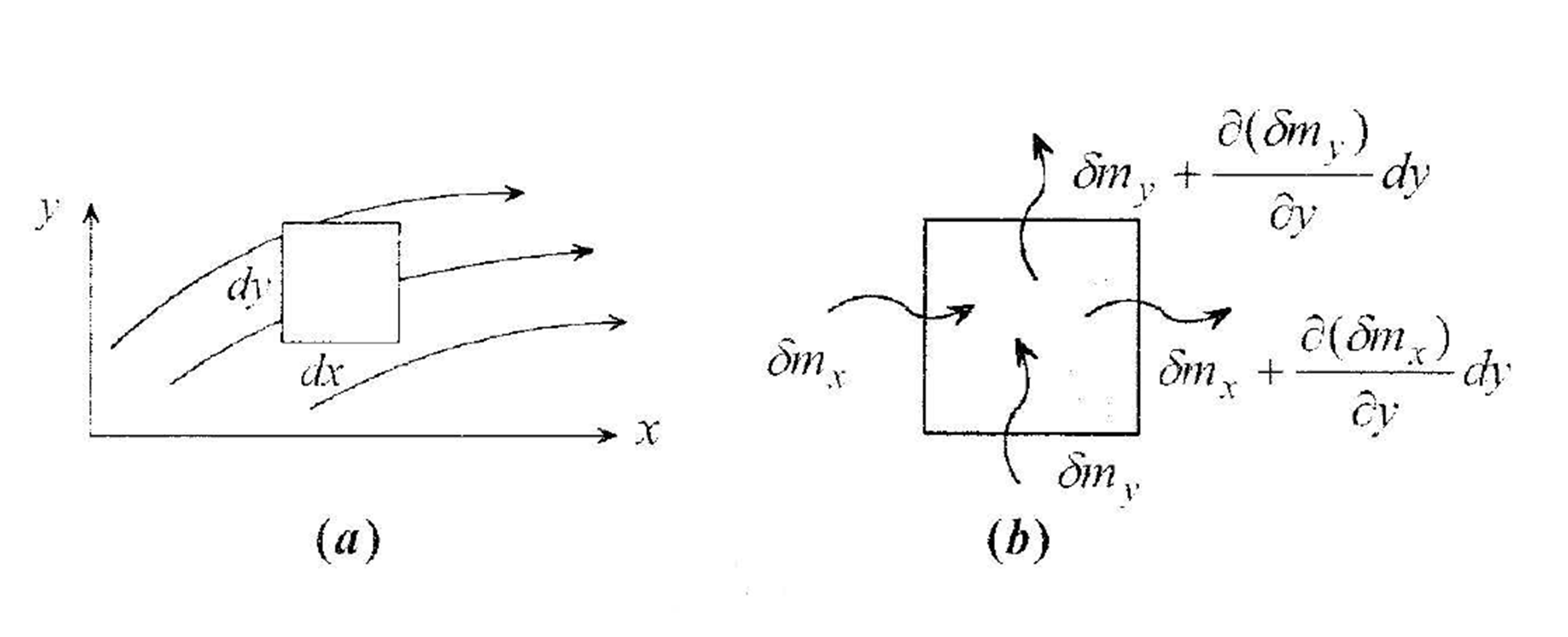
Fig. 29 a) Volumen de control fijo en el espacio donde existe un fluido en movimiento. b) Flujos de masa que entran y salen del volumen de control.

En la figura Fig. 29b, se indica con más detalle el flujo de masa a través de dicho volumen. De esta forma, tenemos

(22)\[\begin{split}\frac{\partial (\delta m)}{\partial t} & = & \delta \dot{m}_x + \delta \dot{m}_y +\delta \dot{m}_z - \left[ \delta \dot{m}_x + \frac{\partial (\delta \dot{m}_x)}{\partial x} dx \right] \\ & & - \left[ \delta \dot{m}_y + \frac{\partial (\delta \dot{m}_y)}{\partial y} dy \right] - \left[ \delta \dot{m}_z + \frac{\partial (\delta \dot{m}_z)}{\partial z} dz \right]\end{split}\]

donde \(\delta m\) es la masa dentro del volumen de control y \(\delta \dot{m}_x\), \(\delta \dot{m}_y\) y \(\delta \dot{m}_z\) son las tasas de cambio de la masa o gasto másico (masa por unidad de tiempo) que entra a dicho volumen en las direcciones \(x\), \(y\) y \(z\), respectivamente. Ya que suponemos que el fluido es un medio continuo, sus propiedades y variables físicas están definidas en cada punto del espacio y a cada tiempo. En particular, la densidad de masa del fluido es una función (campo escalar) de la posición y del tiempo, es decir, \(\rho = \rho \left( x, y, z, t \right)\). Por su parte, la distribución de velocidades en el fluido es un campo vectorial de la forma \(u = \left[ u \left( x, y, z, t \right), v\left( x, y, z, t \right), w \left( x, y, z, t \right) \right]\), donde \(u\), \(v\) y \(w\), son las componentes de la velocidad del fluido en las direcciones \(x\), \(y\) y \(z\), respectivamente. En términos de la densidad, \(\rho\), la masa \(\delta m\) está dada por

(23)\[\delta m = \rho dxdydz\]

mientras que las tasas de cambio de la masa en las distintas direcciones pueden expresarse en términos de \(\rho\) y de las componentes de la velocidad en la forma:

(24)\[\delta \dot{m}_x = \rho u dxdydz\]

(25)\[\delta \dot{m}_y = \rho v dxdydz\]

(26)\[\delta \dot{m}_z = \rho w dxdydz\]

Nótese que el gasto de masa en cada dirección (masa por unidad de tiempo) involucra a la componente de velocidad normal al área por donde atraviesa el fluido. Si sustituimos las ecuaciones (23) y (26) en la ecuación (22) y dividimos entre el volumen \(dx \cdot dy \cdot dz\), obtenemos:

(27)\[\frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x}+ \frac{\partial (\rho v)}{\partial y}+\frac{\partial (\rho w)}{\partial z}=0.\]

Esta ecuación diferencial parcial establece la conservación de la masa en cada punto del fluido y se conoce también como la ecuación de continuidad. Utilizando notación vectorial, se puede expresar en la forma:

(28)\[\frac{\partial \rho}{\partial t} = - {\boldsymbol \nabla} \cdot (\rho {\boldsymbol u} ),\]

donde aparece el operador divergencia aplicado al vector \(\rho {\boldsymbol u} \). Otra manera alternativa de expresar esta ecuación se obtiene al desarrollar las derivadas en la ecuación (27):

(29)\[\frac{\partial \rho}{\partial t} + u\frac{\partial \rho}{\partial x}+v\frac{\partial \rho}{\partial y}+w\frac{\partial \rho}{\partial z} + \rho \left[ \frac{\partial u}{\partial x}+ \frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right]=0,\]

que puede ponerse en la forma

(30)\[\frac{D \rho}{D t} + \rho {\boldsymbol \nabla} \cdot {\boldsymbol u} =0,\]

donde utilizamos el operador derivada material

\[\frac{D }{D t} = \frac{\partial }{\partial t}+u\frac{\partial}{\partial x}+v\frac{\partial}{\partial y}+w\frac{\partial}{\partial z}=\frac{\partial }{\partial t} + {\boldsymbol u} \cdot {\boldsymbol \nabla}\]

El término \(D\rho/Dt\) en la ecuación (30) representa el cambio total de \(\rho\) en un volumen de control que se desplaza junto con el fluido.

Veamos ahora cómo podemos interpretar a la divergencia del campo de velocidades. De la ecuación (28) tenemos:

(31)\[{\boldsymbol \nabla} \cdot {\boldsymbol u} = -\frac{1}{\rho} \frac{D \rho}{D t}.\]

Ahora expresemos esta ecuación en términos del volumen por unidad de masa, es decir, el volumen específico \(\upsilon\) definido como

\[\upsilon = \frac{V}{m} = \rho^{-1}\]

donde \(V\) y \(m\) son el volumen y la masa de cualquier elemento de fluido. Sustituyendo en la ecuación (31) obtenemos

(32)\[{\boldsymbol \nabla} \cdot {\boldsymbol u} = -\upsilon \frac{D \upsilon^{-1}}{D t} =\frac{1}{\upsilon} \frac{D \upsilon}{D t}\]

de donde encontramos que la divergencia del campo de velocidades es igual a la tasa de cambio del volumen del elemento de fluido por unidad de volumen, es decir, la cantidad \({\boldsymbol \nabla} \cdot {\boldsymbol u}\) mide la rapidez con que cambia el volumen de un elemento de fluido (por unidad de volumen).

En general, la densidad de los fluidos depende de su estado termodinámico y para un fluido simple es función de la presión y la temperatura. La relación entre estas variables termodinámicas se denomina ecuación de estado:

\[\rho = \rho \left( p, T \right) \]

La ecuación de estado más sencilla corresponde cuando la densidad del fluido se mantiene constante independientemente de su presión y temperatura, de modo que

\[\frac{D \rho}{D t}=0 \]

Este es un caso particular, pero muy importante, en donde el volumen de un elemento de fluido no puede modificarse. Un fluido que cumple con la condición \(\rho ={\rm constante}\) se denomina un fluido incompresible. El que la densidad sea constante implica que es independiente de la temperatura y la presión, lo que estrictamente es sólo una aproximación, pues todos los fluidos, en mayor o menor medida, modifican su densidad al variar las condiciones termodinámicas. Estrictamente en un fluido incompresible las perturbaciones dentro del mismo se propagan de manera instantánea, es decir, con velocidad infinita. Es común que al abrir repentinamente la puerta de una habitación observemos que las cortinas que se encuentran en el lado opuesto se muevan instantáneamente. En realidad, la perturbación causada al abrir la puerta ocasiona que el aire se mueva con una velocidad mucho menor que la velocidad del sonido en el mismo medio (que es de 340 m/s), por lo que el aire de la habitación se comporta como si fuera incompresible.

Esto sucede en muchos casos de interés práctico en donde las velocidades involucradas son mucho menores que la velocidad del sonido en el medio, en tales casos la aproximación \(\rho ={\rm constante}\) puede considerarse válida. Si esta condición se cumple, la ecuación de conservación de masa (31) se simplifica a la forma:

(33)\[{\boldsymbol \nabla} \cdot {\boldsymbol u} = 0\]

es decir, en un fluido incompresible el campo de velocidades tiene divergencia cero. Físicamente, esta condición implica que un elemento de fluido cualquiera no puede cambiar su volumen. La ecuación de conservación de la masa es una ecuación escalar, es decir, tiene una sola componente. En dos dimensiones, la ecuación (33) toma la forma

(34)\[\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}=0.\]

Aunque los efectos de compresibilidad pueden ser importantes en algunos problemas, como la propagación del sonido, en este curso consideraremos principalmente fluidos incompresibles, teniendo en cuenta que en un gran número de aplicaciones prácticas el agua y el aire pueden considerarse incompresibles.

Tubos de corriente

Consideremos la ecuación de conservación de masa en la forma:

(35)\[\frac{\partial \rho}{\partial t} = - {\boldsymbol \nabla} \cdot (\rho {\boldsymbol u} )\]

e integrémosla en un volumen de control \(V\) fijo en el espacio

\[\frac{\partial }{\partial t} \int_V \rho dV = - \int_V {\boldsymbol \nabla} \cdot (\rho {\boldsymbol u} ) dV\]

donde la integral de la densidad en \(V\) que aparece del lado izquierdo es la masa de fluido contenida en el volumen a un instante dado. Por otra parte, utilizando el teorema de Gauss, podemos escribir la integral del lado derecho de la ecuación anterior como una integral de superficie, es decir,

(36)\[\frac{\partial }{\partial t} \int_V \rho dV = - \int_S \rho {\boldsymbol u} \cdot {\boldsymbol n} dS\]

donde \(S\) es la superficie que encierra al volumen \(V\) y \({\boldsymbol n}\) es la normal a la superficie. Notemos que la integral de superficie es justamente el gasto másico (kg/m\(^3\)) que atraviesa la superficie, de modo que la ecuación (36), indica que la razón de cambio temporal de la masa en el volumen \(V\) es igual al flujo de masa que atraviesa la superficie \(S\), ya sea entrando o saliendo del volumen a través de \(S\). Dicho en otras palabras, esta ecuación nos dice que la masa contenida en \(V\) solo puede cambiar debido a que salga o entre masa al volumen ya que ésta no se puede crear ni destruir.

Consideremos ahora el caso particular en el que el flujo es estacionario de manera que el término del lado izquierdo de la ecuación (36) es cero, entonces:

(37)\[\int_S \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = 0.\]

Supongamos que la superficie \(S\) encierra a un \(\textit {tubo de corriente}\), es decir, a un tubo formado por líneas de corriente, como el mostrado en la figura Fig. 30.

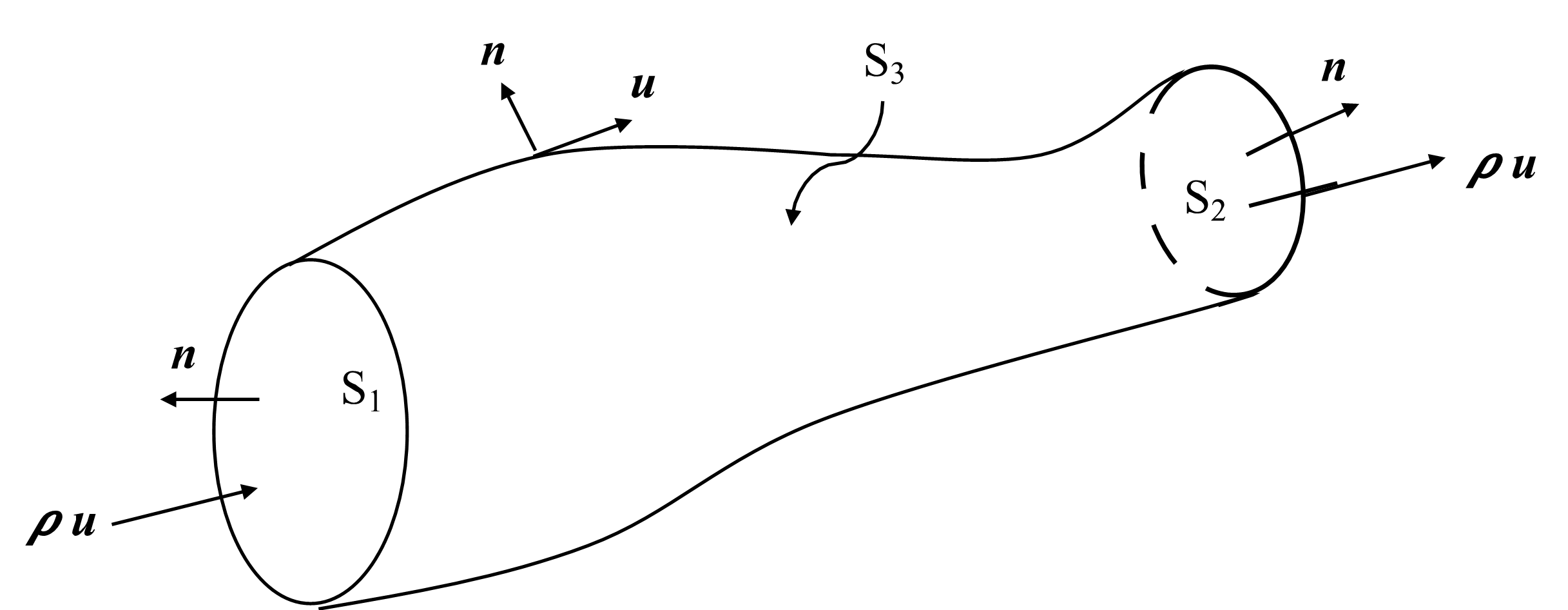
Fig. 30 Un tubo de corriente está formado por líneas de corriente

La integral (37) se puede descomponer en tres contribuciones

(38)\[\int_{S_1} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS +\int_{S_2} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS + \int_{S_3} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = 0.\]

donde \(S_1\) y \(S_2\) corresponden a las superficies de las tapas del tubo mientras que \(S_3\) es su superficie lateral. Ya que ésta se forma por líneas de corriente cuyas tangentes en cada punto coinciden con la velocidad, tenemos

\[\int_{S_3} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = 0,\]

ya que \({\boldsymbol u} \cdot {\boldsymbol n} =0\) pues \({\boldsymbol u}\) y \({\boldsymbol n}\) siempre son ortogonales. Por tanto, (38) se reduce a

(39)\[\int_{S_1} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS +\int_{S_2} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = 0.\]

Ya que la normal en la tapa izquierda apunta en dirección negativa, tenemos:

\[\int_{S_1} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = -\dot{m}_1, \]

mientras que en la tapa derecha

\[\int_{S_2} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS = \dot{m}_2, \]

donde \(\dot{m}_1\) y \(\dot{m}_2\) son los gastos másicos que atraviesan las superficies \(S_1\) y \(S_2\), por lo que concluimos que

\[\dot{m}_1 = \dot{m}_2 \]

es decir, en un flujo compresible en estado estacionario el gasto másico se conserva en cada sección del tubo de corriente.

Es conveniente escribir este resultado en términos de cantidades promedio. En las secciones \(S_1\) y \(S_2\), el promedio del flujo másico se expresa como:

\[\rho_1 u_1 = \frac{1}{S_1} \int_{S_1} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS \]

\[\rho_2 u_2 = \frac{1}{S_2} \int_{S_2} \rho {\boldsymbol u} \cdot {\boldsymbol n} \;dS \]

donde \(\rho_1\), \(u_1\) y \(\rho_2\), \(u_2\) son los valores promedio de la densidad y la velocidad en la secciones \(S_1\) y \(S_2\), respectivamente. Por lo tanto, tenemos

(40)\[\rho_1 u_1 S_1 = \rho_2 u_2 S_2.\]

De manera general podemos decir que para cualquier flujo compresible en estado estacionario se cumple

\[\rho u S = {\rm constante} \]

Si el fluido es incompresible, \(\rho_1=\rho_2=\rho={\rm constante}\), de modo que la ecuación (40) se reduce a

(41)\[ u_1 S_1 = u_2 S_2.\]

es decir, cuando el fluido es incompresible se conserva el gasto volumétrico. Es importante mencionar que los resultados anteriores son válidos únicamente cuando la velocidad del fluido es mucho menor que la velocidad del sonido.

\(\textbf{La función de corriente}\)

Cuando consideramos un flujo en dos dimensiones, la condición de incompresibilidad (34) permite introducir una función escalar conocida como \(\textit {la función de corriente}\), \(\psi\), a partir de la cual podemos expresar las componentes de la velocidad en la forma

(42)\[u = \frac{\partial \psi}{\partial y}, \;\;\;\;\; v = -\frac{\partial u}{\partial x},\]

ya que si sustituimos estas componentes en la ecuación (34) encontramos que se satisface idénticamente:

\[\frac{\partial }{\partial x} \left( \frac{\partial \psi}{\partial y} \right) + \frac{\partial }{\partial y}\left( -\frac{\partial \psi}{\partial x} \right) =0. \nonumber\]

Como veremos más adelante, la función de corriente es muy útil para describir flujos incompresibles en dos dimensiones. Veamos ahora algunas propiedades de esta función.

La primera propiedad es que las líneas \(\psi ={\rm constante}\) corresponden a líneas de corriente del campo de flujo. Ya que \(\psi=\psi(x,y)\), al tomar la diferencial encontramos

\[d\psi = \frac{\partial \psi}{\partial x} dx + \frac{\partial \psi}{\partial y} dy \]

y haciendo uso de las ecuaciones (42),

\[d\psi = -v dx + u dy. \]

Si consideramos que \(\psi ={\rm constante}\), tenemos \(d\psi=0\), es decir,

\[0= -v dx + u dy, \]

o bien,

\[\left( \frac{dy}{dx}\right)_{\psi={\rm cte.}} = \frac{v}{u} \]

que puede expresarse como:

\[\frac{dx}{u} =\frac{dy}{v}, \]

que es precisamente la definición de las líneas de corriente.

Otra propiedad de la función de corriente es que la diferencia entre los valores de dos líneas de corriente da el volumen de fluido que pasa entre las dos líneas de corriente. Consideremos dos líneas de corriente definidas por los valores \(\psi=\psi_1\) y \(\psi_2\) y una superficie de control arbitraria que las une en los puntos \(A\) y \(B\), como se muestra en la figura Fig. 31.

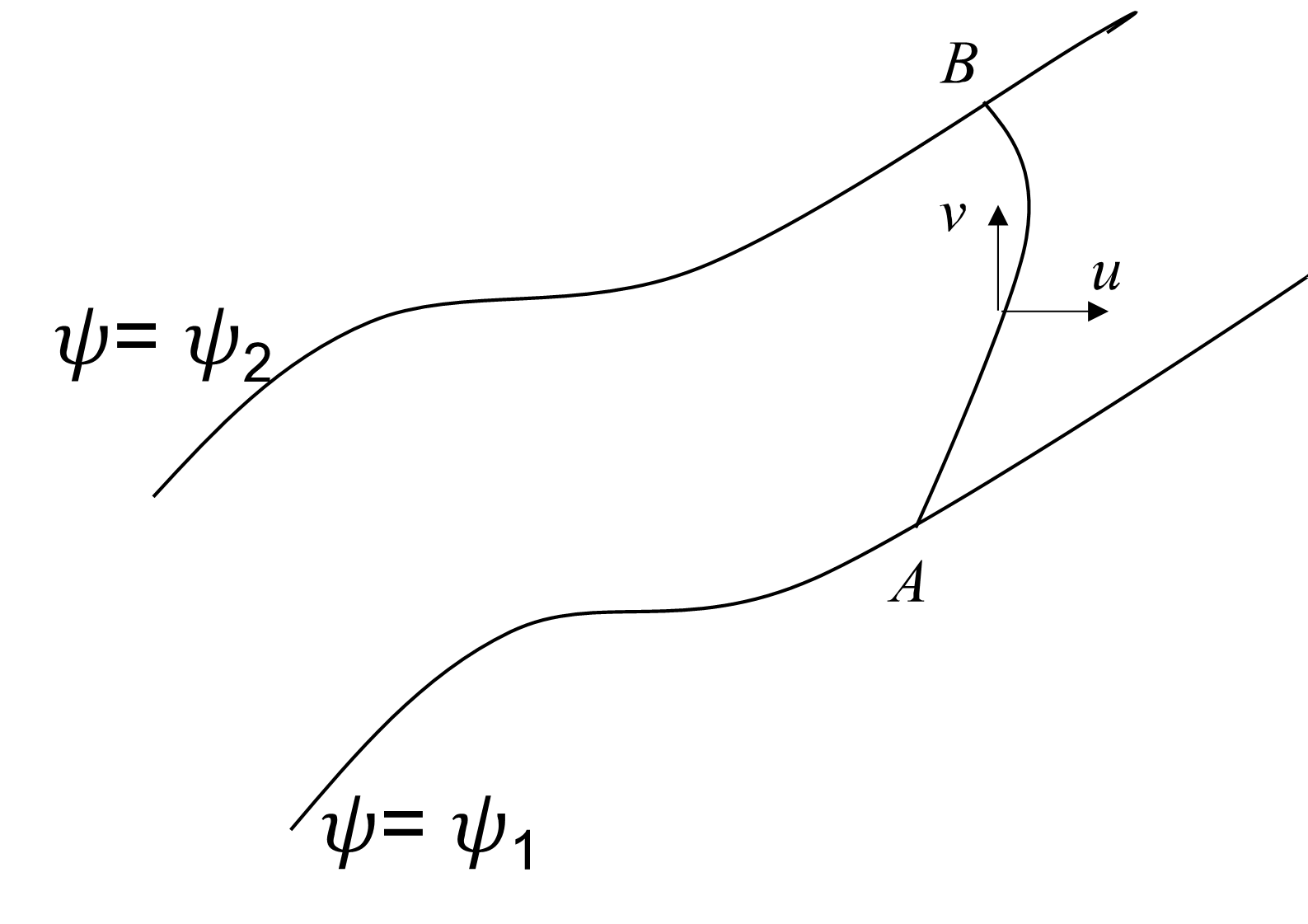
Fig. 31 a) Dos líneas de corriente y una superficie de control arbitraria que las une.

El volumen total de fluido por unidad de tiempo que pasa entre las dos líneas de corriente es

(43)\[Q = \int_s {\boldsymbol u} \cdot {\boldsymbol n} dS = \int_A^B u dy - \int_A^B v dx. \]

Por otro lado, tenemos que

\[d\psi = -v dx + u dy, \]

por lo que al integrar de \(A\) a \(B\)

(44)\[ \int_A^B d\psi = \psi_2 -\psi_1 = -\int_A^B v dx + \int_A^B u dy, \]

y comparando las ecuaciones (43) y (44) encontramos

\[\psi_2 - \psi_1 = Q. \]

Obtengamos ahora la función de corriente de algunos flujos sencillos.

Flujo uniforme. Consideremos un flujo uniforme de magnitud \(U\) y paralelo al eje \(x\), tal que las componentes de la velocidad se expresan en la forma:

\[u= U = \frac{\partial \psi}{\partial y}, \]

\[v= 0 = -\frac{\partial \psi}{\partial x}. \]

Para encontrar la función de corriente integramos la primera ecuación:

\[\frac{\partial \psi}{\partial y} = U \qquad \Rightarrow \qquad \psi = \int U dy = Uy + f(x), \]

donde \(f(x)\) es una función a determinar. Usando la otra ecuación encontramos

\[v= -\frac{\partial \psi}{\partial x} = - \frac{d f}{d x} = 0, \]

de donde obtenemos \(f(x) = C={\rm cte.}\), es decir,

\[\psi = Uy + C \]

Ya que \(C\) es solo una constante aditiva, podemos considerarla igual a cero sin problema. Para determinar las líneas de corriente hacemos \(\psi=\psi_0 = {\rm cte.}\), es decir,

\[\psi_0 = U y \qquad \Rightarrow \qquad y = \frac{\psi_0}{U} \]

lo cual significa que las líneas de corriente son rectas paralelas al eje \(x\) (\(y={\rm cte}\)), donde cada valor de \(\psi_0\) determina una línea de corriente.

Flujo cortante. Consideremos ahora un flujo paralelo al eje \(x\) que crece linealmente con la distancia vertical de modo que las componentes de velocidad son:

\[u= \beta y, \qquad v=0, \]

donde \(\beta\) es una constante. Este es el tipo de flujo que podemos denominar cortante. Para determinar la función de corriente hacemos:

\[u = \beta y = \frac{\partial \psi}{\partial y}, \]

de modo que al integrar con respecto a \(y\) obtenemos

\[\psi = \beta \frac{y^2}{2} + f(x), \]

y usando la segunda componente

\[v= -\frac{\partial \psi}{\partial x} = - \frac{d f}{d x} = 0, \]

de donde nuevamente encontramos \(f(x) = C={\rm cte.}\), es decir,

\[\psi = \beta \frac{y^2}{2} + C. \]

y podemos considerar \(C=0\). Las líneas de corriente las encontramos haciendo \(\psi=\psi_0={\rm cte.}\), esto es,

\[\beta \frac{y^2}{2} =\psi_0 \quad \Rightarrow \quad y = \sqrt{\frac{2\psi_0}{\beta}}, \]

de modo que, nuevamente las líneas de corriente son líneas horizontales paralelas al eje \(x\).

Flujo con un punto de estancamiento. En este caso el campo de velocidades es

\[{\boldsymbol u} = (-\alpha x, -\alpha y), \]

de donde

\[u = \frac{\partial \psi}{\partial y} = \alpha x \quad \Rightarrow \quad \psi = \int \alpha x dy = \alpha xy + f(x). \]

De la otra componente tenemos:

\[v= -\frac{\partial \psi}{\partial x} = -\alpha y - \frac{d f}{d x} = 0, \]

pero ya que \(v= -\alpha y\), \(df/dx=0\) por lo que \(f\) es una constante que podemos tomar como cero, de modo que

\[\psi = \alpha xy \]

Las líneas de corriente \(\psi=\psi_0=\)constante son

\[\psi_0 = \alpha xy\]

de donde

\[y= \frac{\psi_0/\alpha}{x},\]

es decir, son hipérbolas como lo habíamos determinado previamente.

Flujo en rotación de cuerpo rígido. Como vimos previamente, el campo de velocidades se expresa como

\[{\boldsymbol u} = (-\Omega y, -\Omega x),\]

entonces:

\[u = \frac{\partial \psi}{\partial y} = -\Omega y \quad \Rightarrow \quad \psi = \int \Omega y dy = -\Omega \frac{y^2}{2} + f(x). \]

De la otra componente

\[v= -\frac{\partial \psi}{\partial x} = - \frac{d f}{d x} = \Omega x, \]

de modo que,

\[f(x) = -\Omega \frac{x^2}{2} + C.\]

Haciendo la constante cero, obtenemos la función de corriente:

\[\psi = -\frac{\Omega}{2} \left( x^2 + y^2 \right), \]

de donde las líneas de corriente están dadas por la ecuación:

\[x^2 + y^2 = -\frac{2\psi_0}{\Omega}, \]

es decir, son círculos centrados en el origen con radio igual a \(\sqrt{-2\psi_0/\Omega}\), por lo que la constante \(\psi_0\) sólo puede tomar valores negativos.

También podemos expresar la función de corriente en coordenadas polares. En estas coordenadas la ecuación de continuidad es

(45)\[\frac{1}{r} \frac{\partial (ru_r)}{\partial r} + \frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}=0, \]

por lo que definiendo las componentes de la velocidad en la forma:

\[u_r=\frac{1}{r} \frac{\partial \psi}{\partial \theta}, \qquad u_{\theta}= -\frac{\partial \psi}{\partial r}, \]

se satisface idénticamente la ecuación (45):

\[\frac{1}{r} \frac{\partial }{\partial r}\left(r \frac{1}{r} \frac{\partial \psi}{\partial \theta} \right) + \frac{1}{r} \frac{\partial }{\partial \theta} \left(-\frac{\partial \psi}{\partial r} \right)=0. \]

En estas coordenadas el flujo en rotación de cuerpo rígido tiene las componentes:

\[u_r =0, \qquad u_{\theta} = \Omega r, \]

de modo que,

\[u_{\theta}= -\frac{\partial \psi}{\partial r} = -\Omega r \quad \Rightarrow \quad \psi = \int \Omega r dr = -\Omega \frac{r^2}{2} + f(\theta), \]

y de la componente radial encontramos

\[u_r=\frac{1}{r} \frac{\partial \psi}{\partial \theta} = \frac{1}{r} \frac{df}{d\theta}=0 \quad \Rightarrow \quad f={\rm constante}. \]

Igualando la constante a cero obtenemos la función

\[\psi = - \frac{\Omega}{2} r^2, \]

de donde, para \(\psi=\psi_0=\) constante, las líneas de corriente están determinadas por la ecuación del círculo

\[r = \sqrt{\frac{-2\psi_0}{\Omega}}, \quad {\rm con} \quad \psi_0 <0. \]

\(\textbf {Fuente centrada en el origen.}\) El campo de velocidades definido por las componentes

\[u_r = \frac{C}{r}, \qquad u_{\theta} =0, \]

donde \(C\) es una constante positiva, representa a un flujo que emerge del origen fluyendo radialmente. En este caso tenemos

\[u_r=\frac{1}{r} \frac{\partial \psi}{\partial \theta} = \frac{C}{r} \quad \Rightarrow \quad \psi = \int C d\theta = C \theta + f(r), \]

pero

\[u_{\theta}= -\frac{\partial \psi}{\partial r}= -\frac{df}{dr} =0 \quad \Rightarrow \quad f={\rm constante}. \]

por lo que haciendo la constante igual a cero, la función de corriente es

\[\psi = C \theta, \]

y las líneas de corriente son:

\[\psi_0 = C \theta \quad \Rightarrow \quad \theta = \frac{\psi_0}{C}, \]

es decir, son líneas rectas (\(\theta=\)constante) que pasan por el origen. Si la constante \(C\) tomara valores negativos, en vez de tener una fuente, tendríamos un sumidero.