Vorticidad y circulación

Se recomienda al lector ver los siguientes videos realizados por el National Committee for Fluid Mechanics Films (NCFMF) en cooperación con el Education Development Center

Vorticity, Part 1

Vorticity, Part 2

así como las notas de estos materiales, que se pueden pueden consultar en el siguiente enlace: https://web.mit.edu/hml/ncfmf.html.

La vorticidad, \(\boldsymbol{ \omega}\), es un campo vectorial de gran importancia en la mecánica de fluidos y se define como:

\[{\boldsymbol \omega} = {\boldsymbol \nabla} \times {\boldsymbol u}. \]

Un flujo cuya vorticidad es nula se denomina irrotacional, mientras que un flujo con vorticidad distinta de cero se conoce como rotacional. Notemos que la vorticidad es un campo solenoidal:

\[{\boldsymbol \nabla} \cdot {\boldsymbol \omega} = {\boldsymbol \nabla} \cdot {\boldsymbol \nabla} \times {\boldsymbol u} = 0, \]

es decir, su divergencia es cero. En un flujo bidimensional

\[{\boldsymbol u} = [u(x,y,t), v(x,y,t), 0 ], \]

la vorticidad tiene una única componente en la dirección normal al plano del flujo, \({\boldsymbol \omega} = \left( 0,0,\omega_z \right)\), donde

\[\omega_z = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}. \]

Definimos la circulación de un campo de velocidades \({\boldsymbol u}\) alrededor de un circuito \(C\) en la forma

\[\Gamma = \oint_C {\boldsymbol u} \cdot d{\boldsymbol x}, \]

donde \(d{\boldsymbol x}\) es un elemento de línea a lo largo de la curva cerrada \(C\) que yace en la región del fluido. Si hacemos uso del teorema de Stokes, tenemos

\[\Gamma = \oint_C {\boldsymbol u} \cdot d{\boldsymbol x} = \int_S {\boldsymbol \nabla} \times {\boldsymbol u} \cdot {\boldsymbol n} \;dS \]

donde \(S\) es la superficie encerrada por la curva \(C\) y \({\boldsymbol n}\) es la normal a dicha superficie, de modo que podemos expresar la circulación en la forma:

\[\Gamma = \int_S {\boldsymbol \omega} \cdot d{\boldsymbol n} \;dS. \]

Esto indica que si la curva \(C\) encierra a una superficie \(S\) que yace completamente en una región de flujo irrotacional, \(\boldsymbol \omega =0\), la circulación es cero, \(\Gamma=0\).

Interpretación de la vorticidad

A continuación mostraremos que la vorticidad es una medida de la rotación local de un elemento de fluido. Para simplificar el análisis consideremos un flujo en dos dimensiones con un elemento de fluido rectangular que rota como un cuerpo rígido respecto a un eje que apunta en la dirección normal al plano de flujo \(xy\).

Originalmente los elementos de línea ortogonales \(oa\) y \(ob\), que tienen longitudes \(\Delta x\) y \(\Delta y\), respectivamente, se encuentran alineados con las direcciones \(x\) y \(y\) de los ejes coordenados. Después de un tiempo \(\Delta t\), ambos elementos rotan en dirección contraria a las manecillas del reloj manteniéndose siempre ortogonales (ver Fig. 15). Para que esto suceda, en los puntos \(a\) y \(b\) debe existir una velocidad distinta a la del punto \(o\). Para que el punto \(a\) se desplace verticalmente desde el eje \(x\) hasta la línea punteada, la componente de la velocidad en dirección \(y\) debe ser distinta de cero y variar en la dirección \(x\). Si la velocidad en \(o\) es \(v_0\), la velocidad en el punto \(a\) debe ser ligeramente mayor, por lo que se puede expresar como

\[v =v_0 + \Delta v = v_0 + \frac{\partial v}{\partial x} \Delta x. \]

La rotación del elemento de línea genera el ángulo \(\Delta \alpha\) de manera que la velocidad angular de rotación de dicho elemento, \(\dot{\Omega}_{oa}\), es:

\[\dot{\Omega}_{oa} = \lim_{\Delta t \rightarrow 0} \frac{\Delta \alpha}{\Delta t} = \lim_{\Delta t \rightarrow 0} \frac{\Delta \eta/\Delta x}{\Delta t}, \]

donde el ángulo \(\Delta \alpha\) se ha expresado en términos del desplazamiento \(\Delta \eta\) entre el radio de giro \(\Delta x\). Por otro lado, el desplazamiento vertical \(\Delta \eta\) se puede expresar como:

\[\Delta \eta = \Delta v \Delta t = \frac{\partial v}{\partial x} \Delta x \Delta t, \]

de modo que,

\[\dot{\Omega}_{oa} = \lim_{\Delta t \rightarrow 0} \frac{\frac{\partial v}{\partial x} \frac{\Delta x \Delta t}{\Delta x}}{\Delta t}= \frac{\partial v}{\partial x}, \]

es decir, la derivada \(\partial v/\partial x\) se puede interpretar como la velocidad angular instantánea de rotación del elemento de línea \(oa\).

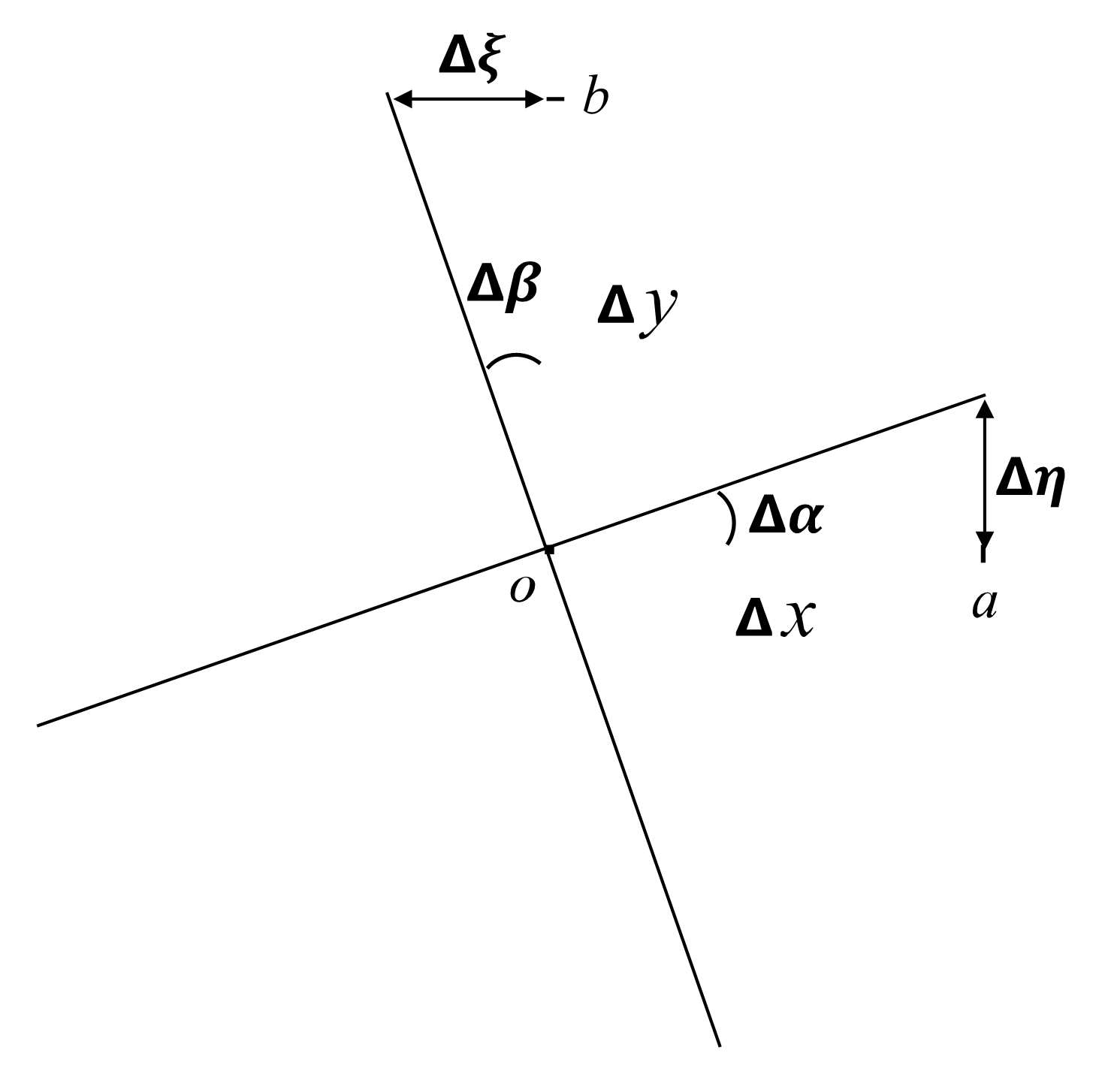
Fig. 15 Rotación de cuerpo rígido de un elemento de fluido rectangular

Si ahora realizamos el mismo análisis para el elemento de línea \(ob\) a lo largo del eje \(y\), vemos que para que el elemento rote la velocidad en dirección \(x\) negativa debe ser distinta de cero y variar a lo largo de \(y\). Si la velocidad en el punto \(o\) es \(u_0\), la velocidad en el punto \(b\) es:

\[u =u_0 + \Delta u = u_0 + \frac{\partial u}{\partial y} \Delta y. \]

Por tanto, la velocidad angular de rotación del elemento \(ob\) es

\[\dot{\Omega}_{ob} = \lim_{\Delta t \rightarrow 0} \frac{\Delta \beta}{\Delta t} = \lim_{\Delta t \rightarrow 0} \frac{\Delta \xi/\Delta y}{\Delta t}, \]

donde el desplazamiento horizontal \(\Delta \xi\) está dado por:

\[\Delta \xi = -\Delta u \Delta t = \frac{\partial u}{\partial y} \Delta y \Delta t, \]

de modo que:

\[\dot{\Omega}_{ob} = \lim_{\Delta t \rightarrow 0} \frac{-\frac{\partial u}{\partial y} \frac{\Delta y \Delta 0}{\Delta y}}{\Delta t}= -\frac{\partial u}{\partial y}, \]

por lo que \(-\partial u/\partial y\) es la velocidad angular de rotación instantánea del elemento \(ob\). Ahora bien, la rotación del elemento rectangular de fluido alrededor del eje \(z\) es el promedio de la velocidad angular instantánea de los elementos de línea \(oa\) y \(ob\) en el plano \(xy\), es decir,

\[\dot{\Omega}_{z} = \frac{1}{2} \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right). \]

Si realizamos el mismo análisis para elementos rectangulares en los planos \(yz\) y \(xz\) encontramos

\[\dot{\Omega}_{x} = \frac{1}{2} \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right), \]

\[\dot{\Omega}_{y} = \frac{1}{2} \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right), \]

es decir, la velocidad angular de rotación de un elemento tridimensional está dada por

\[(\dot{\Omega}_{z}, \dot{\Omega}_{z}, \dot{\Omega}_{z}) = \frac{1}{2}(\omega_x,\omega_y,\omega_z)\]

o bien,

\[\dot{{\boldsymbol \Omega}} = \frac{1}{2} {\boldsymbol \omega}.\]

Vemos entonces que la vorticidad es dos veces la velocidad angular instantánea de rotación de un elemento de fluido \({\boldsymbol \omega}= 2 \dot{{\boldsymbol \Omega}}\). Por tanto, la vorticidad es una medida de la \(\textit{ rotación local}\) de los elementos de fluido, pero \(\textbf{no está relacionada con la rotación global del fluido,}\) ni tampoco tiene relación con la curvatura de las líneas de corriente.

Cuando la vorticidad es cero, es decir \({\boldsymbol \nabla} \times {\boldsymbol u}=0\), se dice que el campo de velocidades es irrotacional. En tal caso, dicho campo necesariamente está dado como el gradiente de una función escalar \(\phi\), es decir,

\[{\boldsymbol u} = {\boldsymbol \nabla} \phi = \left( \frac{\partial \phi}{\partial x}, \frac{\partial \phi}{\partial y}, \frac{\partial \phi}{\partial z}\right), \]

ya que entonces \({\boldsymbol \nabla} \times {\boldsymbol \nabla} \phi ={\boldsymbol 0}\).

La función escalar \(\phi\) se conoce como el \(\textit{ potencial de velocidades}\) y a los flujos que se pueden expresar en la forma \({\boldsymbol u} = {\boldsymbol \nabla} \phi\), se les denomina \(\textit{flujos potenciales}\). Por tanto, los flujos irrotacionales son flujos potenciales.

A continuación mostraremos algunos ejemplos sencillos que ilustran flujos con y sin vorticidad.

\(\textbf{ Flujo rectilíneo cortante}\)

Consideremos un flujo rectilíneo entre dos paredes rígidas (ver Fig. 16), producido por el movimiento de una de ellas con velocidad \(U\), mientra que la otra permanece en reposo. El fluido viscoso inmerso entre las dos paredes se adhiere a ellas, por lo que en la pared superior adquiere la velocidad \(U\), dando lugar a un campo de velocidades de la forma

\[{\boldsymbol u} = \left( U \frac{y}{h}, 0,0 \right) \]

Si calculamos la vorticidad, tenemos

\[{\boldsymbol \omega} = {\boldsymbol \nabla} \times {\boldsymbol u} = \left( 0,0,\omega_z \right), \]

donde

\[\omega_z = \cancel{\frac{\partial v}{\partial x}} - \frac{\partial u}{\partial y} = -\frac{U}{h}, \]

es decir, la vorticidad es negativa y constante lo que nos indica que en cada punto las partículas de fluido rotarán en la dirección de las manecillas del reloj. Esto es esperable ya que si observamos el elemento de fluido cuadrado mostrado en la Fig. 16, la velocidad en la cara superior es mayor a la velocidad en la cara inferior lo que ocasionará que la partícula tienda a girar.

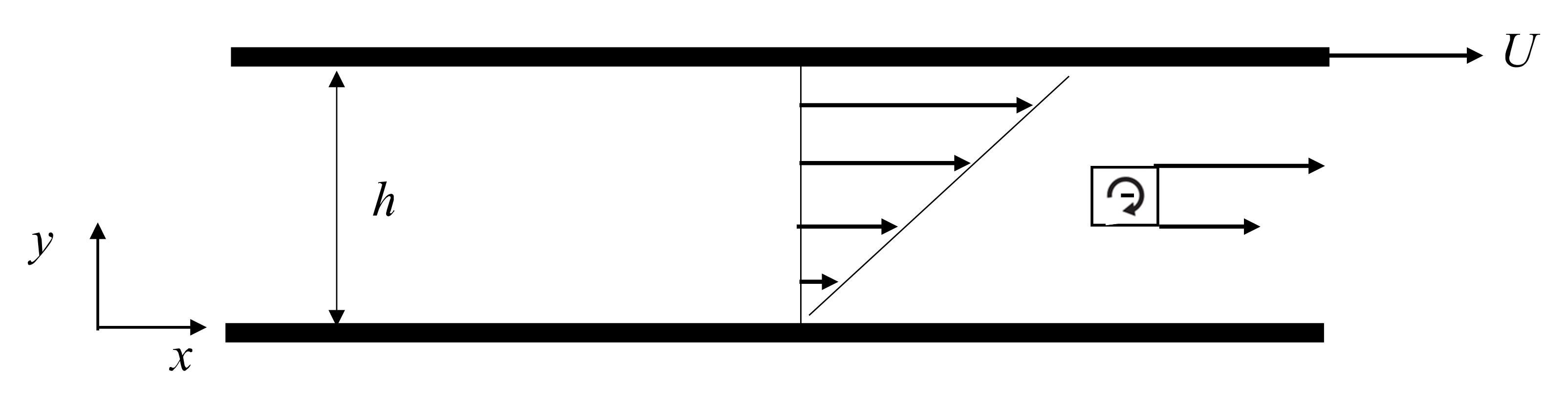
Fig. 16 Flujo rectilíneo cortante de un fluido viscoso producido por el movimiento de una de las paredes que confina al fluido

Si introdujéramos un medidor de vorticidad muy burdo consistente en un corcho que flota en el fluido con una cruz pintada en la parte superior observaríamos el giro horario del medidor. En este caso particular, la vorticidad, y por tanto la velocidad angular de rotación de cualquier partícula de fluido, es constante en cualquier punto. Si ahora calculamos la circulación en un circuito \(C\) de arbitrario dentro del fluido, tenemos

\[\Gamma = \oint_C {\boldsymbol u} \cdot d{\boldsymbol x} = \int_S {\boldsymbol \omega} \cdot {\boldsymbol n} dS = \omega_z \int_S dS = -\frac{U}{h} \; A, \]

Ya que la vorticidad es constante, la circulación es simplemente el producto de \(\omega_z=-U/h\) por el área \(A\) encerrada por el circuito \(C\).

Flujo entre placas paralelas

Consideremos ahora un flujo que tiene lugar entre dos paredes rígidas e infinitas separadas por una distancia \(2h\), como el mostrado en la Fig. 17. El movimiento se da en la dirección del eje \(x\) de manera que el campo de velocidades se expresa como:

\[{\boldsymbol u} = [u(y),0,0], \]

donde:

\[ u(y) = U_{max} \left[ 1 -\left( \frac{y}{h} \right)^2 \right]. \]

Por tratarse de un flujo viscoso, la velocidad se anula en las paredes, es decir, \(u(-h/2)=u(h/2)=0\).

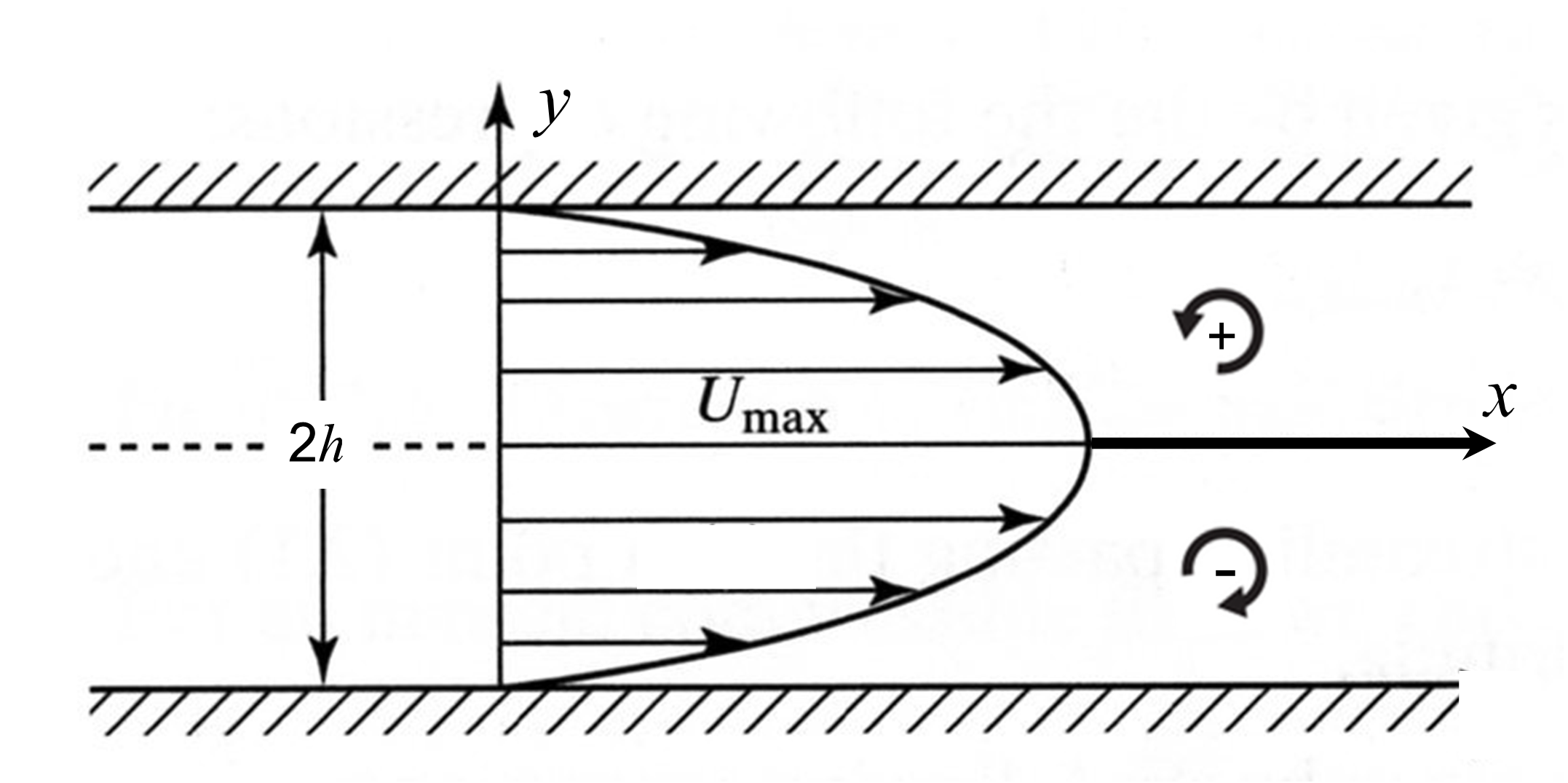
Fig. 17 Flujo entre paredes rígidas paralelas. La vorticidad depende de la posición vertical y es positiva en la sección superior y negativa en la inferior

Al igual que en el ejemplo anterior, la única componente de la vorticidad es \(\omega_z\) y tiene el valor:

\[\omega_z = - \frac{\partial u}{\partial y} = 2u_{max} \frac{y}{h}, \]

de manera que \(\omega_z\) depende de la posición, tomando valores positivos en la mitad superior y negativos en la inferior. Por tanto, un medidor de vorticidad girará en sentido antihorario en la parte superior (i.e. con vorticidad positiva) y en sentido horario en la parte inferior (i.e. con vorticidad negativa). Nótese que justo en \(y=0\) la vorticidad se anula. Si calculamos la circulación en un circuito de forma rectangular, encontramos:

\[\begin{split}\Gamma &= \int_S {\boldsymbol \omega} \cdot {\boldsymbol n} dS = \int_{x_1}^{x_2} \int_{y_1}^{y_2} \omega_z(y) \;dx \;dy \nonumber \\ &= \frac{2u_{max}}{h} \int_{x_1}^{x_2} \int_{y_1}^{y_2} y \; dx \;dy = \frac{2u_{max}}{h^2} (x_2-x_1)\; \frac{(y_2^2-y_1^2)}{2}. \nonumber\end{split}\]

Estos ejemplos muestran que aún en flujos rectilíneos puede existir vorticidad, ya que ésta es una característica local del flujo que manifiesta la rotación de las partículas de fluido, independientemente de si el flujo presenta una rotación global.

Flujo en rotación de cuerpo rígido

Analicemos ahora la vorticidad en el flujo en rotación de cuerpo rígido cuyo campo de velocidades en coordenadas cartesianas se expresa en la forma

\[{\boldsymbol u} = (-\Omega y, \Omega x ). \]

Como vimos previamente, este es un flujo estacionario con líneas de corriente (y trayectoria) circulares por lo que es conveniente realizar su descripción utilizando coordenadas polares. De manera general, la transformación entre las componentes cartesianas \((u,v)\) y las componentes polares \((u_r,u_{\theta})\) de un campo de velocidades es:

(18)\[u= u_r \cos \theta + u_{\theta} \cos \left( \frac{\pi}{2} - \theta \right) = u_r \cos \theta - u_{\theta} \; {\rm sen} \; \theta\]

(19)\[ v= u_r \; {\rm sen} \; \theta + u_{\theta} \; {\rm sen} \; \left( \frac{\pi}{2} - \theta \right) = u_r \; {\rm sen} \; \theta + u_{\theta} \cos \theta\]

donde \(\theta\) es el ángulo que forma la componente radial con el eje horizontal (ver Fig. 18).

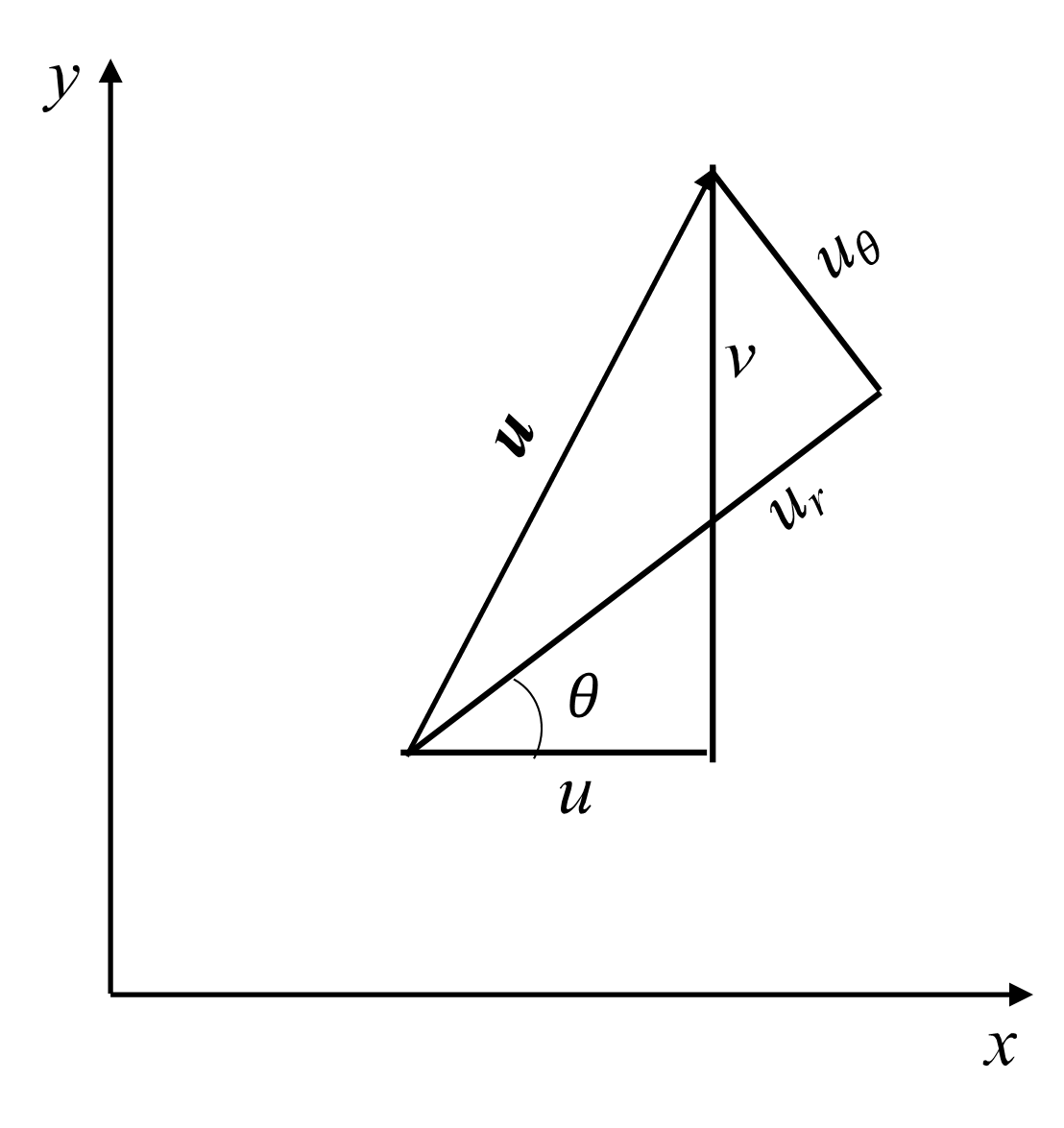
Fig. 18 Descomposición del vector de velocidad \({\boldsymbol u}\) en coordenadas Cartesianas \((u,v)\) y en coordenadas polares \((u_r, u_{\theta})\)

Si invertimos las ecuaciones anteriores obtenemos:

(20)\[u_r= u \cos \theta + v \; {\rm sen} \; \theta,\]

(21)\[u_{\theta} =- u \; {\rm sen} \; \theta + v \cos \theta.\]

Para el flujo en rotación de cuerpo rígido tenemos \(u=-\Omega y\) y \(v=\Omega x\), de modo que utilizando las ecuaciones (20) y (21) encontramos:

\[\begin{split}u_r &= -\Omega y \cos \theta + \Omega x \; {\rm sen} \; \theta = -\Omega r \; {\rm sen}\; \theta \cos \theta + \Omega r \cos \theta \; {\rm sen} \; \theta =0 \nonumber \\ u_{\theta} &= \Omega y \; {\rm sen} \theta + \Omega x \cos \theta = \Omega r \; {\rm sen}^2 \; \theta + \Omega r \cos^2 \theta = \Omega r \nonumber\end{split}\]

donde hemos usado que \(x=r\cos \theta\) y \(y=r {\rm sen} \;\theta\), por lo que el campo de velocidades en coordenadas polares se expresa como \({\boldsymbol u} = (0, \Omega r )\), es decir, la velocidad tangencial es proporcional a la distancia radial.

En coordenadas cilíndrico-polares, la vorticidad la podemos calcular en la forma:

\[\begin{split}{\boldsymbol \omega} = {\boldsymbol \nabla} \times {\boldsymbol u} = \frac{1}{r} \begin{vmatrix} {\boldsymbol e}_r & r{\boldsymbol e}_{\theta} & {\boldsymbol e}_z\\ \frac{\partial}{\partial r} & \frac{\partial}{\partial \theta} & \frac{\partial}{\partial z}\\ u_r & ru_{\theta} & u_z \end{vmatrix}\end{split}\]

de donde

\[{\boldsymbol \omega} = \frac{1}{r} \left[ \left( \frac{\partial u_z}{\partial \theta} - \frac{\partial (ru_{\theta})}{\partial z} \right) {\boldsymbol e}_r +\left( \frac{\partial u_r}{\partial z} - \frac{\partial u_z}{\partial r} \right) r {\boldsymbol e}_{\theta} + \left( \frac{\partial (ru_{\theta})}{\partial r} - \frac{\partial u_r }{\partial \theta} \right) {\boldsymbol e}_z. \right]\]

Dado que el flujo tiene lugar en el plano \(xy\), la única componente de la vorticidad es \(\omega_z\), es decir,

\[\omega_z = \frac{1}{r} \left( \frac{\partial (ru_{\theta})}{\partial r} - \cancel{\frac{\partial u_r }{\partial \theta}} \right) = \frac{1}{r} \frac{\partial (\Omega r^2)}{\partial r} = 2 \Omega. \]

Esto muestra que la velocidad angular de rotación de cada elemento de fluido alrededor de su propio eje es igual a \(\Omega\). Curiosamente, la velocidad de rotación de una partícula alrededor del eje \(z\) centrado en el origen es también \(\Omega\), es decir, el periodo de tiempo para completar una rotación de la partícula alrededor de su propio eje es igual al tiempo requerido para realizar una rotación alrededor del origen. La Fig. 19 muestra el comportamiento de un medidor de vorticidad en este flujo.

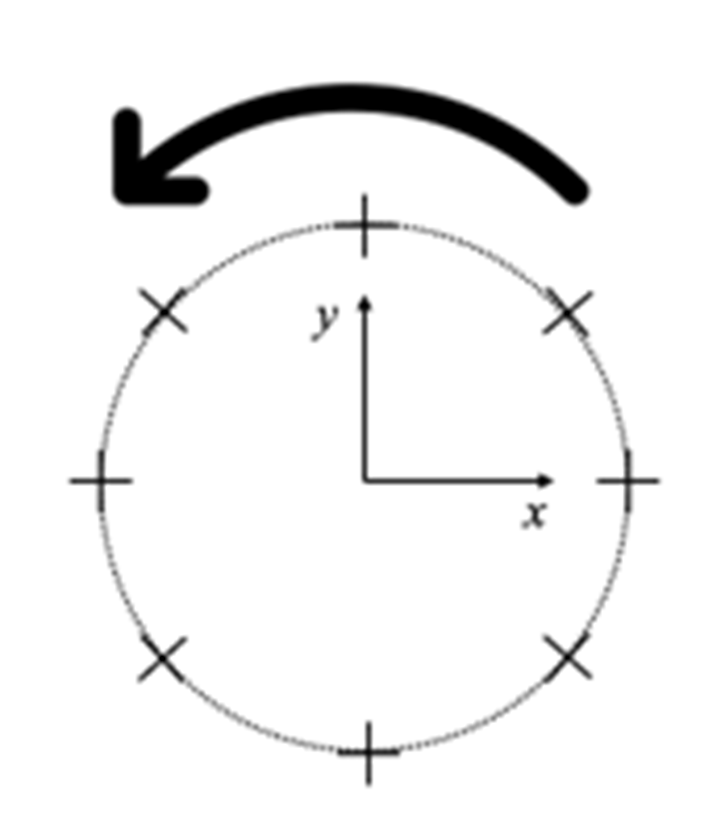
Fig. 19 En el flujo en rotación de cuerpo rígido un medidor de vorticidad \(\large{+}\) se desplaza siguiendo una trayectoria circular a la vez que rota alrededor de su propio eje.

Si calculamos la circulación alrededor de cualquier circuito de radio \(r\) obtenemos:

\[\Gamma = \oint_C {\boldsymbol u} \cdot d{\boldsymbol x} = \int_0^{2\pi} u_{\theta} \; r \;d\theta = 2\pi r u_{\theta} = 2 \Omega \;(\pi r^2), \]

es decir,

\[\Gamma = {\rm vorticidad} \; \times \; {\rm area}, \]

lo que se cumple para cualquier circuito en el fluido independientemente de si contiene, o no, al origen.

\(\textbf{ Vórtice ideal}\)

Analicemos otro flujo con líneas de corriente circulares. En este caso, las componentes de velocidad en coordenadas polares son:

\[u_r =0, \;\;\;\;\;\;\;u_{\theta} = \frac{K}{r}, \]

donde \(K\) es una constante. Mientras que en el flujo en rotación de cuerpo rígido, la velocidad tangencial varía linealmente con \(r\), en este caso es inversamente proporcional a \(r\), por lo que al tender la distancia radial a cero la velocidad crece sin restricción. Al calcular la vorticidad encontramos:

\[\omega_z = \frac{1}{r} \left( \frac{\partial (ru_{\theta})}{\partial r} \right) = \frac{1}{r} \frac{\partial }{\partial r}\left(r \frac{K}{r} \right) = 0, \]

lo cual es válido para todo \(r \neq 0\), por lo que el flujo es irrotacional, excepto en el origen donde la vorticidad está indeterminada. Si calculamos la circulación alrededor de cualquier circuito que no encierre al origen, será cero puesto que la vorticidad también es cero. Por otro lado, si calculamos la circulación alrededor de un circuito que encierre al origen, por ejemplo, un contorno circular de radio \(r\), tenemos:

\[\Gamma = \int_0^{2\pi} u_{\theta} r d\theta = \int_0^{2\pi} \left(\frac{K}{r}\right) r d\theta = 2\pi K, \]

lo que muestra que \(\Gamma\) es constante e independiente del radio del contorno. De hecho, la circulación es igual a \(2\pi K\) alrededor de cualquier circuito de forma arbitraria que encierre al origen. Mientras que la vorticidad está indeterminada en el origen, circulación alrededor de cualquier circuito que lo encierre es finita. Para interpretar este resultado podemos expresar la circulación para este flujo en la forma:

\[\Gamma = \int_S {\boldsymbol \omega} \cdot {\boldsymbol n} dS, \]

donde \(S\) es una superficie que contiene al origen. El lado izquierdo de esta ecuación es distinto de cero por lo que \({\boldsymbol \omega}\) debe ser distinto de cero dentro de \(S\). Ya que \(\Gamma\) es independiente de \(r\), podemos reducir el circuito que encierra a \(S\) sin alterar \(\Gamma\). En el límite, cuando el área encerrada se aproxima a cero, necesariamente la vorticidad debe tender a infinito de manera que \(\Gamma\) se mantenga constante. Es decir, si \(\delta {\boldsymbol S}\) es el elemento de superficie que encierra al origen, cuando \(\delta {\boldsymbol S} \rightarrow 0\), necesariamente \({\boldsymbol \omega} \rightarrow \infty\) de modo que:

\[{\boldsymbol \omega} \cdot \delta {\boldsymbol S} = {\rm constante} = \Gamma. \]

El vórtice ideal es entonces un flujo en donde toda la vorticidad está localizada en el origen siendo irrotacional en cualquier otro punto. Si colocamos un medidor de vorticidad en este flujo encontraremos que se desplazará alrededor del origen en una trayectoria circular, sin embargo no rotará alrededor de su propio eje, como se muestra en la Fig. 20.

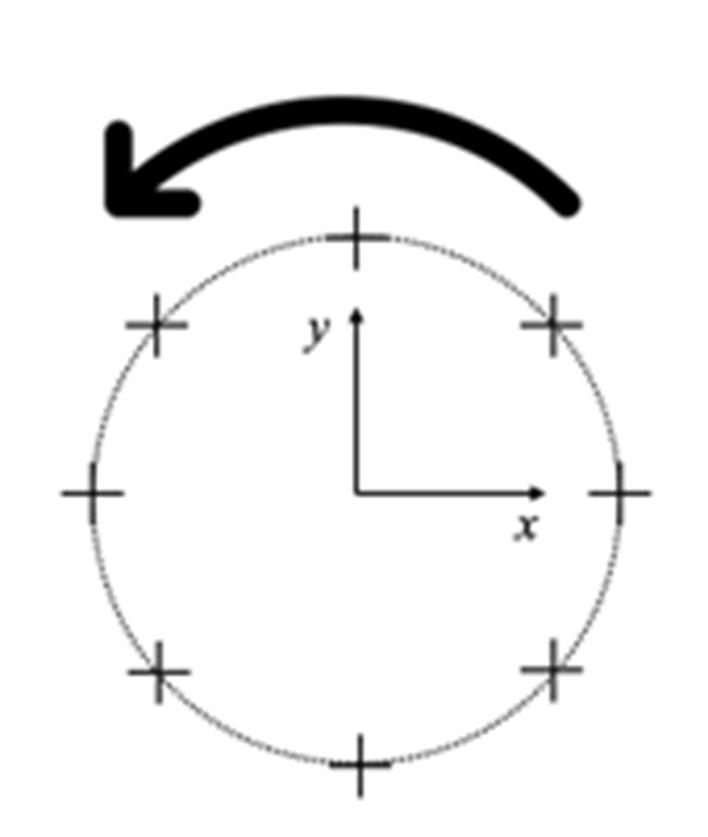
Fig. 20 En un vórtice ideal un medidor de vorticidad \(\large{+}\) se desplaza siguiendo una trayectoria circular pero sin rotar alrededor de su propio eje. En este vórtice toda la vorticidad se concentra en el origen.

\(\textbf{ Vórtice de Rankine}\)

El que un vórtice ideal tenga una velocidad que tiende a infinito en el origen impide su utilización en la modelación de fenómenos reales. Los vórtices que observamos en la Naturaleza, como un ciclón atmosférico o un remolino en el océano, tienen un núcleo donde la velocidad alcanza valores finitos y presenta, aproximadamente, una rotación de cuerpo rígido, mientras que fuera de él, el campo de velocidades es cercanamente irrotacional.

El vórtice de Rankine es un modelo sencillo que presenta un comportamiento más cercano a los vórtices que se observan en la realidad. Se compone de un núcleo, que se extiende hasta un radio \(r=a\), que gira como un cuerpo rígido, fuera del cual la velocidad tangencial es la de un vórtice ideal (ver Fig. 21). Matemáticamente lo podemos expresar en la forma:

\[\begin{split}u_{\theta} = \left \{ \begin{matrix} \Omega r & \mbox{si } r < a, \\ \\ \frac{\Omega a^2}{r} & \mbox{si } r > a. \end{matrix}\right.\end{split}\]

Notamos que mientras que la velocidad es cero en el origen, justo en la frontera \(r=a\) toma el valor \(\Omega a\). La existencia del núcleo rotacional garantiza que tanto la velocidad como la vorticidad, tomen valores finitos.

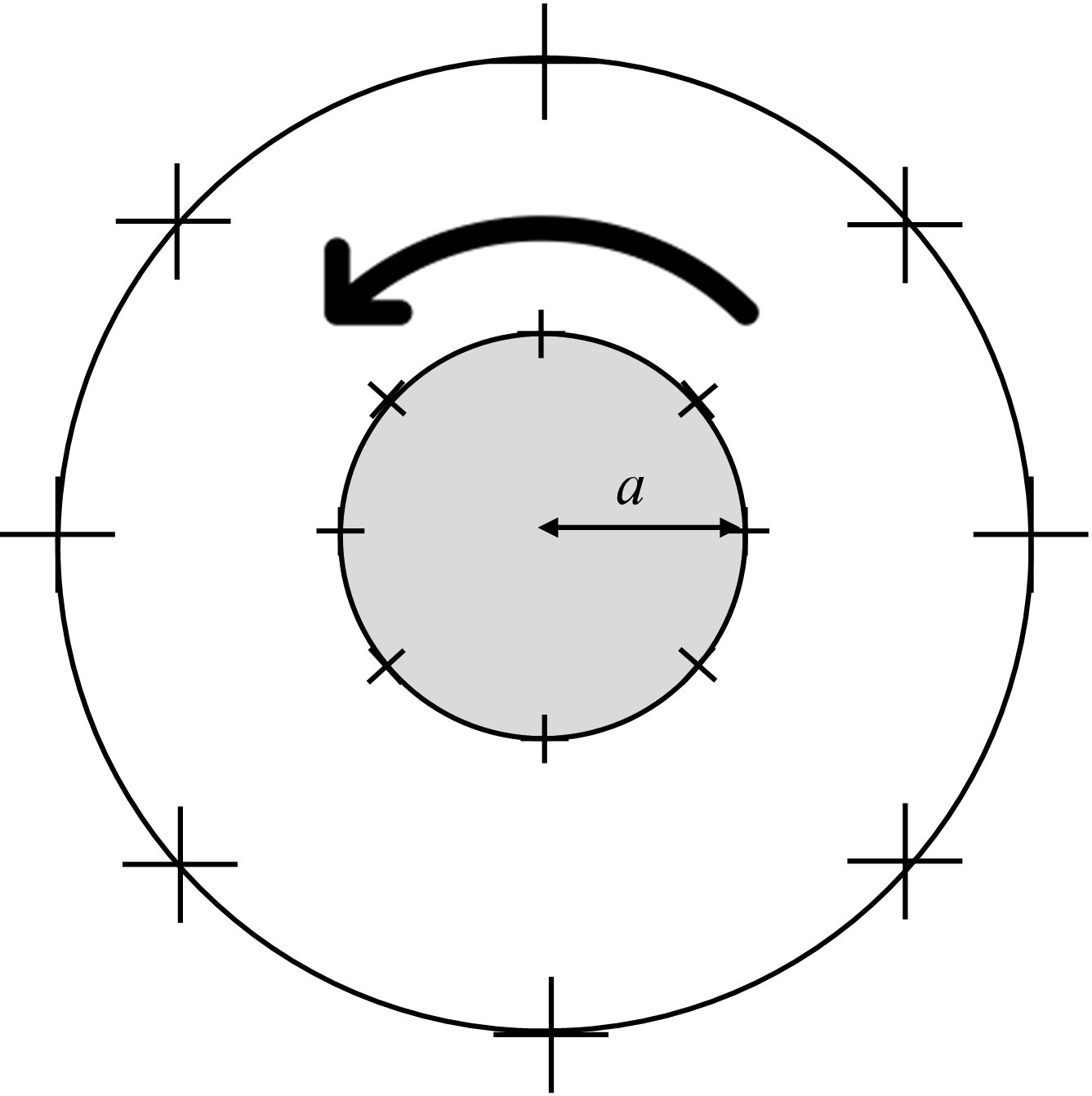
Fig. 21 El vórtice de Rankine tiene un núcleo de radio \(a\) que rota como un cuerpo rígido mientras que para \(r>a\), el fluido se comporta como un vórtice ideal.

La Fig. 22 y Fig. 23 muestra los perfiles de velocidad y vorticidad en un vórtice de Rankine. La velocidad tangencial crece linealmente en el núcleo y después decae como \(1/r\), mientras que la vorticidad toma un valor constante en el núcleo y es cero fuera de él. En este vórtice, la transición entre el núcleo y el exterior se da de manera abrupta, lo que no sucede en un vórtice real.

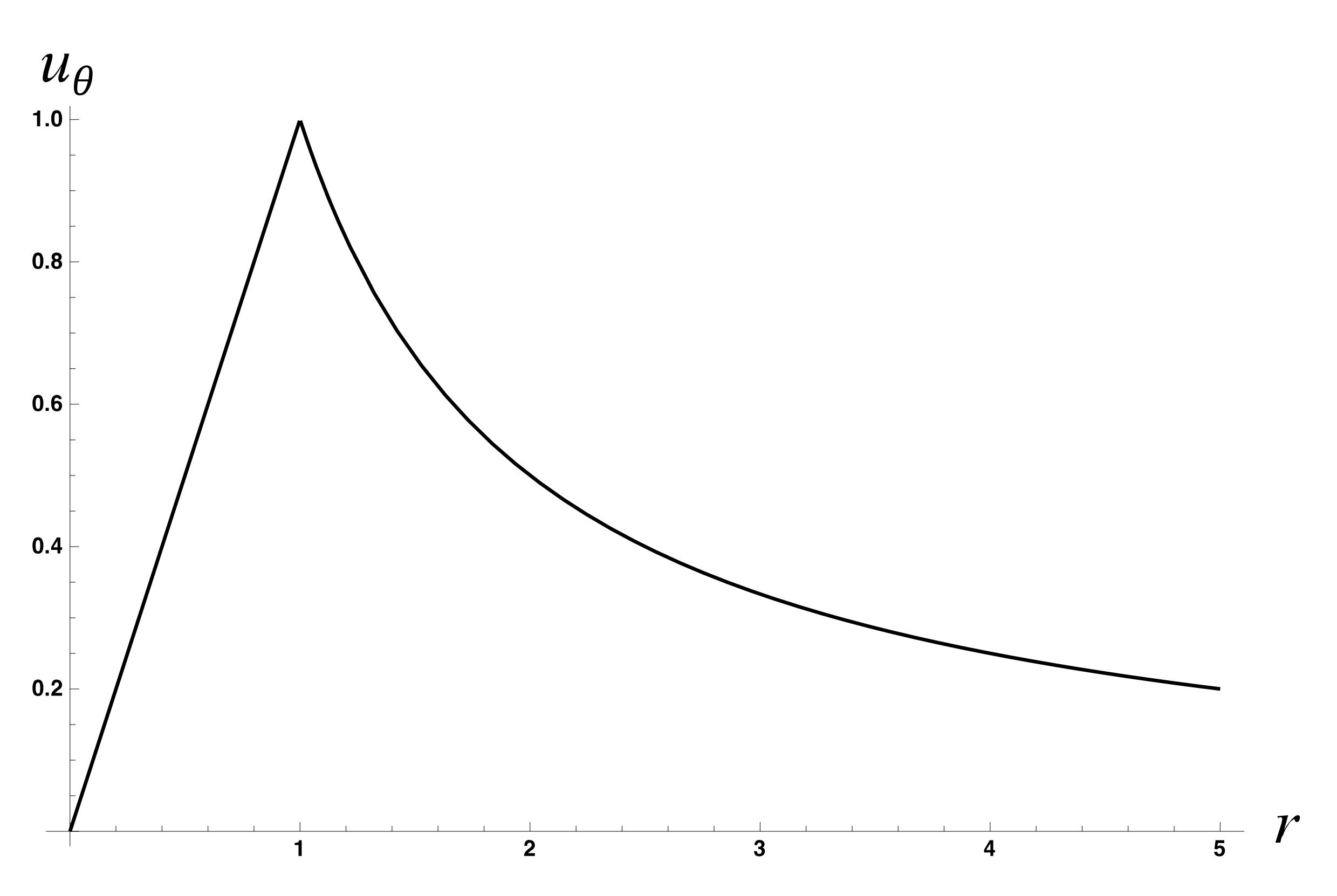
Fig. 22 Perfil de velocidades de un vórtice de Rankine con un núcleo que se extiende hasta \(r=1\) y cuya velocidad angular de rotación es \(\Omega=1\).

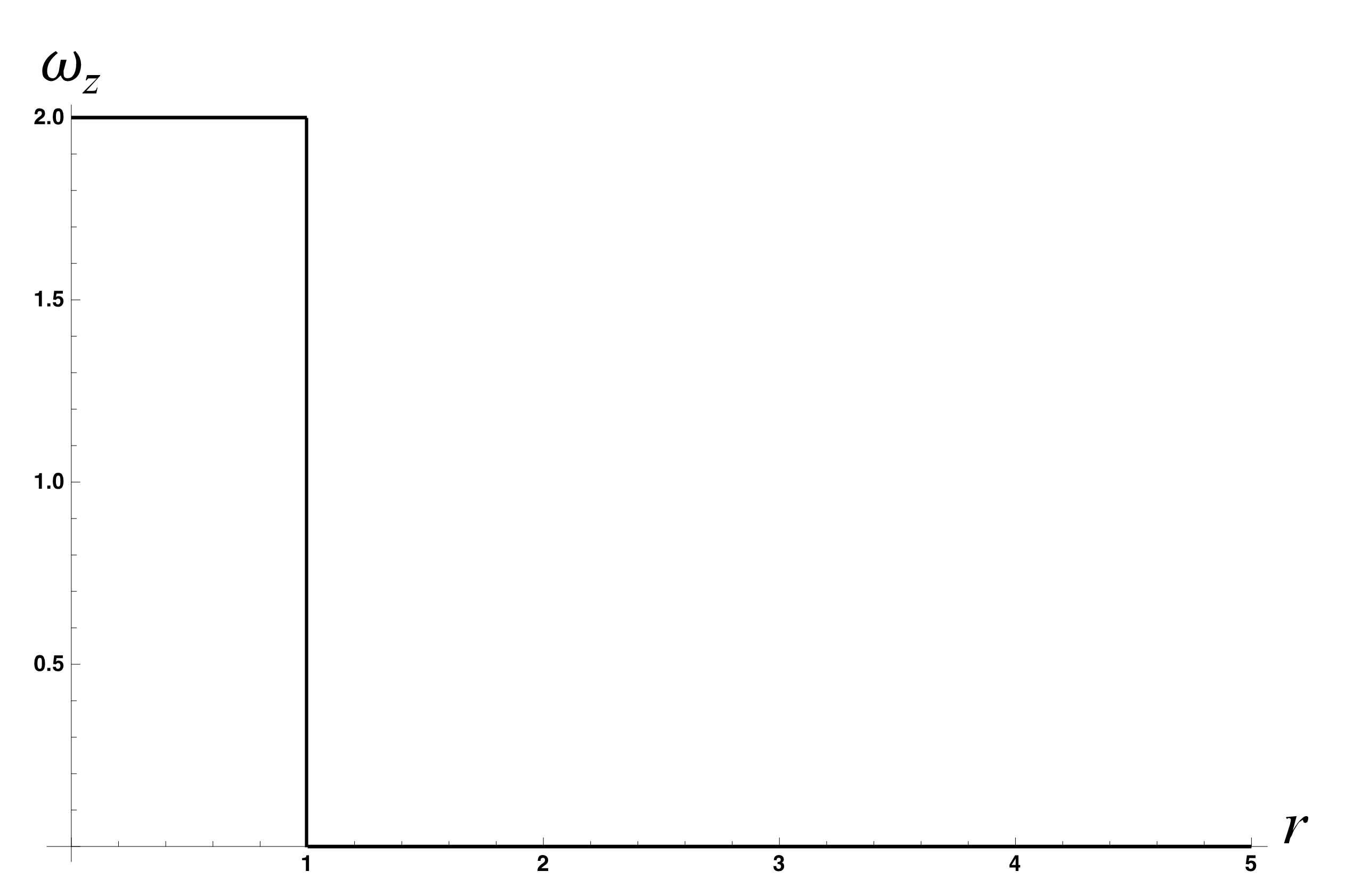
Fig. 23 Vorticidad de un vórtice de Rankine con un núcleo que se extiende hasta \(r=1\) y cuya velocidad angular de rotación es \(\Omega=1\).

Existen diferentes modelos de vórtices que reproducen de mejor manera el comportamiento de vórtices reales. Por ejemplo, el vórtice Kepleriano, utilizado en la modelación de la formación de sistemas planetarios [7], se expresa como:

\[u_{\theta} = \frac{k}{\sqrt{r}} \left\{ 1- \exp\left[ - \left(\frac{r}{R}\right)^{3/2} \right] \right\} \]

donde \(k\) y \(R\) son constantes, siendo \(R\) la extensión del núcleo. Calculando la vorticidad encontramos:

\[\omega_z = \frac{1}{r} \frac{\partial (ru_{\theta})}{\partial r} = \frac{k}{2r^{3/2}} \left\{ 1- \left( 1-3 \left( \frac{r}{R} \right)^{3/2} \right) \exp\left[ - \left(\frac{r}{R}\right)^{3/2} \right] \right\}. \]

La figura Fig. 24 y Fig. 25 muestra los perfiles de velocidad y vorticidad para un vórtice Kepleriano donde la transición entre el núcleo y el exterior se da de una manera más suave que en el vórtice de Rankine.

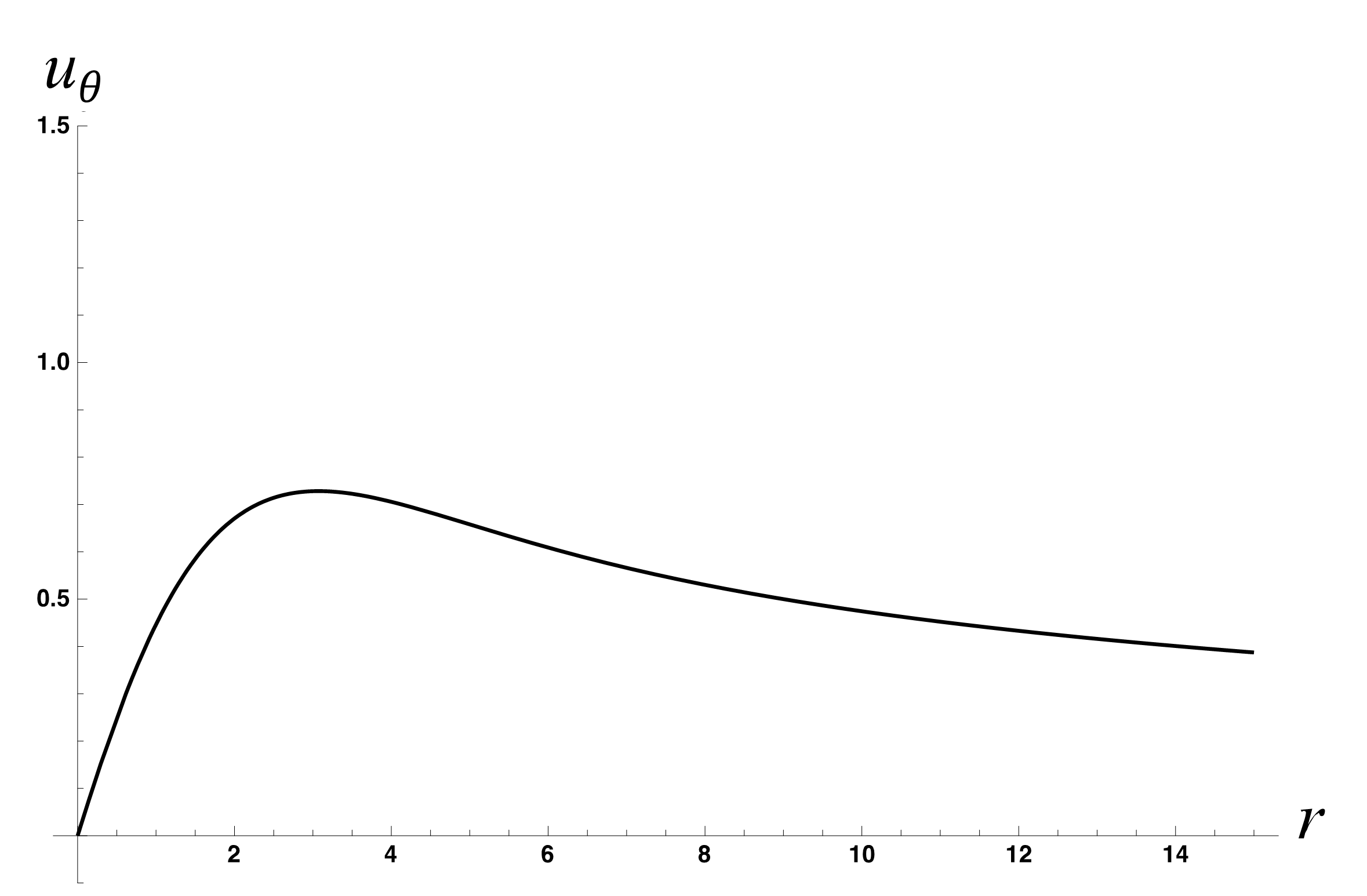
Fig. 24 Perfil de velocidades de un vórtice Kepleriano con un núcleo que se extiende hasta \(r=2\). El valor de la constante \(k\) es 1.5

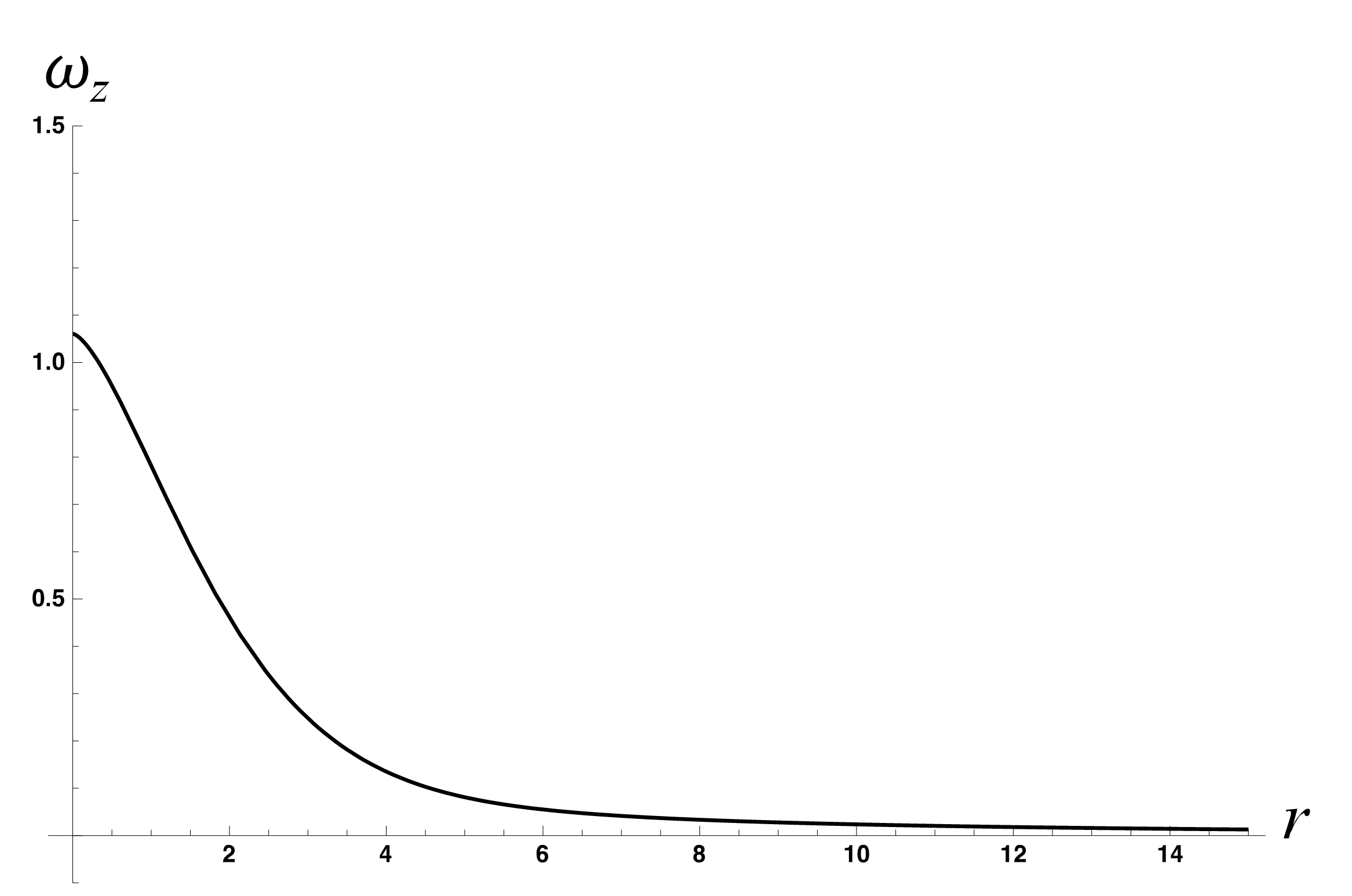
Fig. 25 Vorticidad de un vórtice Kepleriano con un núcleo que se extiende hasta \(r=2\). El valor de la constante \(k\) es 1.5