Flotación: el principio de Arquímedes

Es una experiencia cotidiana observar objetos que flotan en el agua y otros que se hunden. De igual forma, observamos que un globo lleno de helio asciende en la atmósfera, de manera similar a como una pelota llena de aire asciende en el agua después de haber sido sumergida. Para efectuar la descripción del estado de reposo o movimiento de un objeto en contacto con uno o más fluidos debemos hacer uso de las leyes de movimiento de Newton. Consideremos un ejemplo sencillo en donde un cubo de paredes rígidas se encuentra flotando completamente sumergido en un fluido, por ejemplo, agua (ver Fig. 48) y analicemos cuáles son las fuerzas que actúan sobre él.

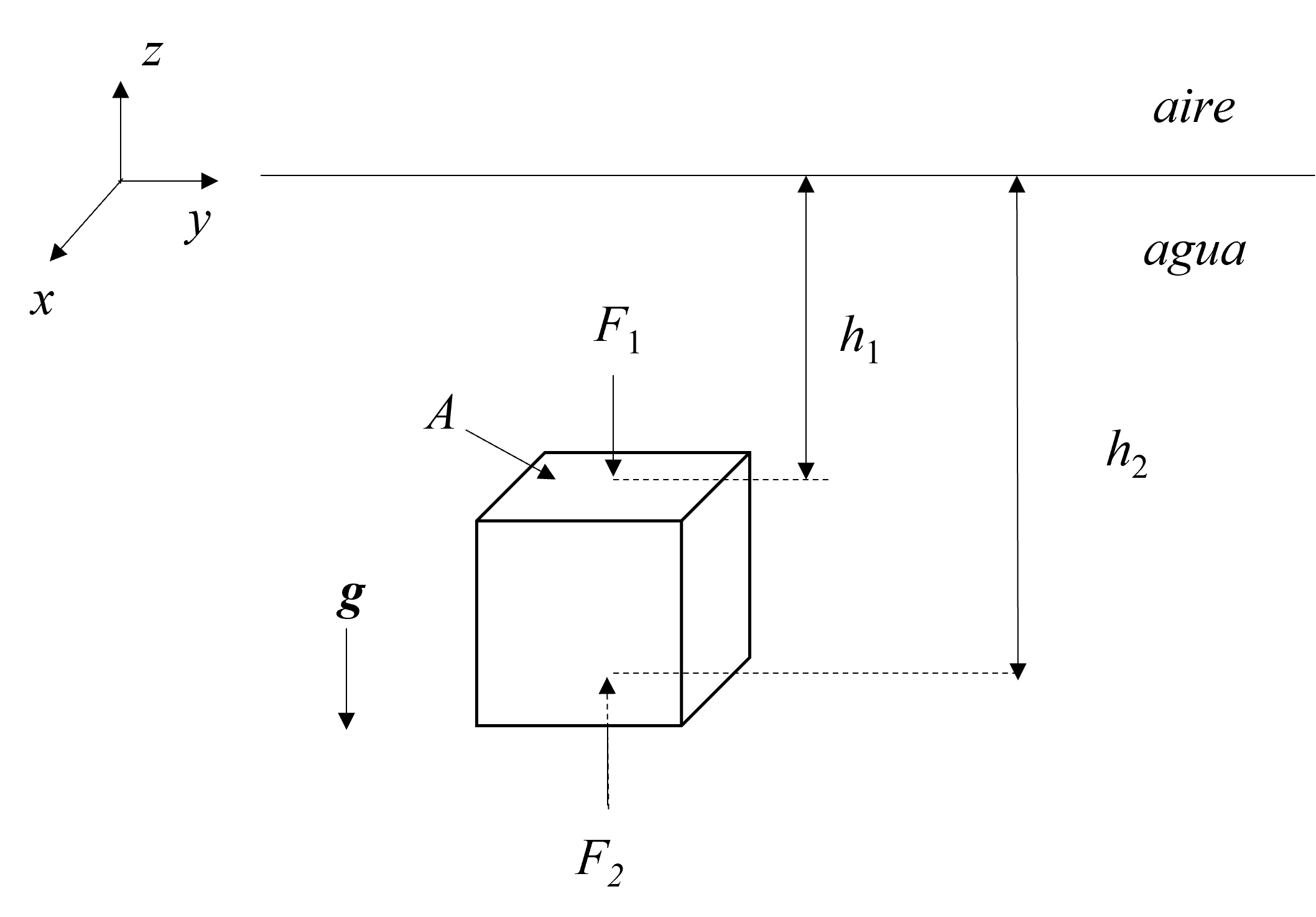
Fig. 48 Cuerpo sólido de forma cúbica sumergido en agua.

Evidentemente, la gravedad actúa sobre el objeto ejerciendo una fuerza (el peso) hacia abajo y puesto que se encuentra flotando debe existir una fuerza que comprense al peso para mantener al objeto en reposo. Esta fuerza es ejercida por la presión sobre las paredes del cubo. Primero notemos que sobre cada par de paredes laterales existen fuerzas de presión que se compensan exactamente. Por otra parte, sobre la pared superior del cubo que se encuentra a una distancia \(h_1\) de la superficie del agua actúa una fuerza hacia abajo que es igual a la presión que ejerce la columna de agua multiplicada por el área, \(A\), de la cara del cubo, es decir,

(115)\[F_{1}=\rho gh_{1}A\]

A su vez, sobre la cara inferior que se encuentra a una profundidad \(h_{2}\) por debajo de la superficie, actúa una fuerza hacia arriba igual al producto de la presión ejercida por la columna de agua por el área de la cara, esto es

(116)\[F_{2}=\rho gh_{2}A\]

De modo que la fuerza neta de superficie ejerecida sobre las paredes del cubo es

(117)\[F_{e}=F_{2}-F_{1}=\rho g\left(h_{2}-h_{1}\right)A\]

Esta fuerza es conocida como empuje y evidentemente es positiva (hacia arriba) ya que \(h_{2}>h_{1}\). Notemos que \(V=A(h_{2}−h_{1}\)) es precisamente el volumen del cubo de modo que podemos expresar el empuje como

(118)\[F_{e}=\rho gV\]

donde \(\rho V\) es justamente la masa del fluido desalojado. El volumen \(V\) se conoce como el volumen desalojado o desplazado que en este caso coincide con el volumen total del cubo puesto que está totalmente sumergido. Es importante notar que cuando el objeto se encuentra totalmente sumergido, el empuje será el mismo independiente de la produndidad de inmersión puesto que el empuje solo depende del volumen desplazado de fluido. La fuerza de empuje existe por el hecho de que el fondo de un objeto está siempre más sumergido en el fluido que su parte superior, y ya que la presión se incrementa con la profundidad, la fuerza de presión hacia abajo que se ejerce sobre la superficie superior del cuerpo será menor que la fuerza de presión hacia arriba que se ejerce sobre su superficie inferior. Este resultado se conoce como el principio de Arquímedes y puede enunciarse de la siguiente manera:

Un cuerpo inmerso parcial o totalmente en un fluido experimenta una fuerza de flotacion vertical igual al peso del fluido desplazado, con dicha fuerza actuando a través del centro de gravedad del fluido desplazado.

Notemos que la fuerza de flotación o empuje existirá siempre sobre el objeto inmerso en un fluido idependientemente de que el objeto flote o se hunda. Cuando un cuerpo flota, el empuje se iguala exactamente con su peso. Si el cuerpo se hunde, el peso es mayor que el empuje. Puede mostrarse que la fuerza de flotación o empuje actúa a través del centroide del volumen de fluido desplazado.

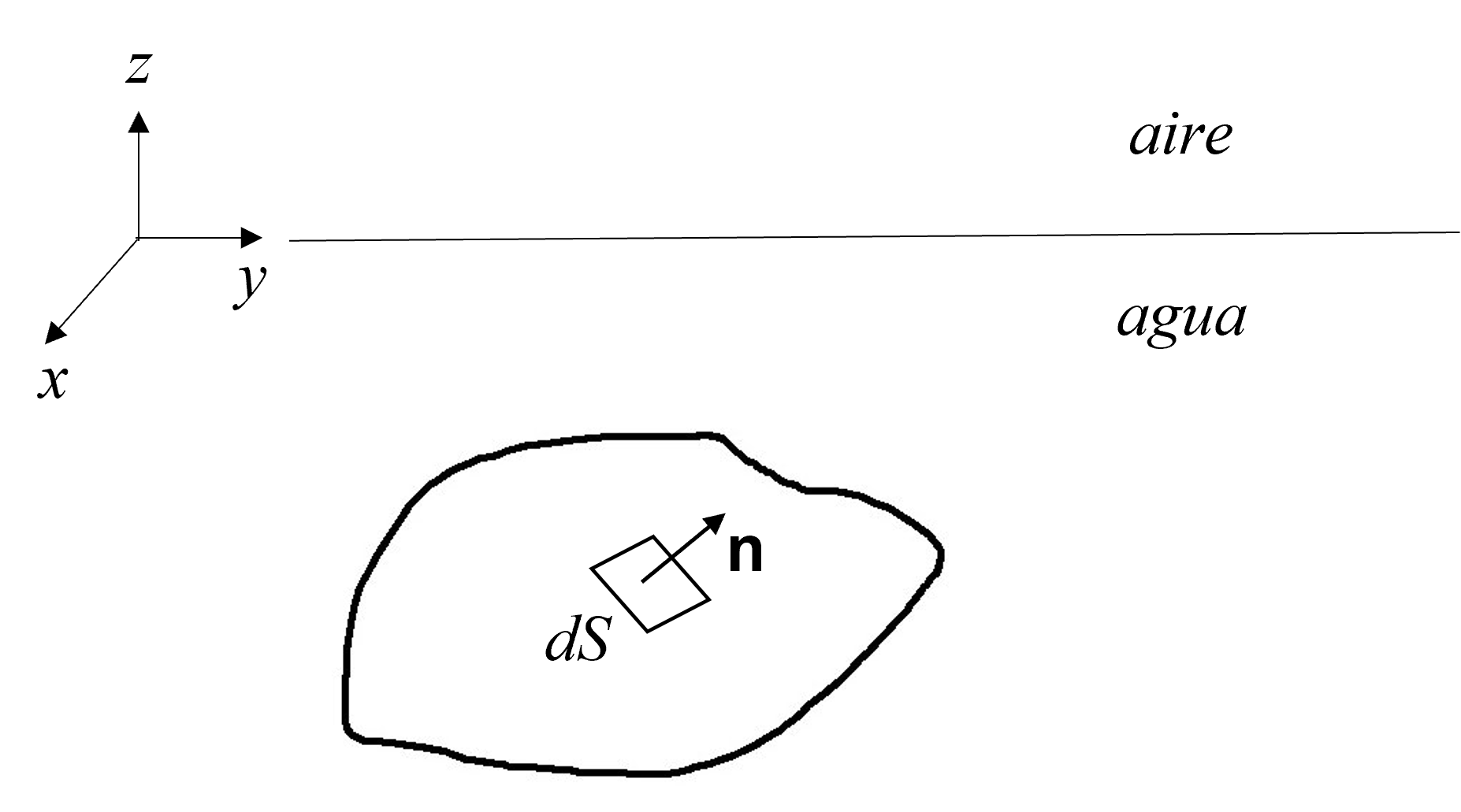
Fig. 49 Cuerpo sólido de forma arbitraria sumergido en agua.

El razonamiento anterior que nos llevó a enunciar el pricipio de Arquímedes se basó en considerar un cuerpo con una forma particular. A continuación mostraremos que este principio es independiente de la forma que tenga el cuerpo. Consideremos un cuerpo de forma arbitraria sumergido en un fluido en reposo, como se muestra en la Fig. 49. Podemos calcular la fuerza de superficie que actúa sobre el objeto integrando la presión en toda su superficie. La diferencial de fuerza sobre un elemento de superficie \(dS\) esta dada por:

(119)\[dF=-pndS\]

donde n es el vector normal a la superficie y el signo menos indica que la fuerza de presión actua hacia el interior del cuerpo. Si integramos la ecuación anterior sobre toda la superficie del objeto, tenemos

(120)\[F=-\int_{s}pndS\]

Para calcular la integral haremos uso de una generalización del teorema de Gauss. Para un campo vectorial B este teorema establece que

(121)\[\int_{s} B \cdot p n dS = \int_{V} \nabla \phi dV\]

donde \(V\) es el volumen encerrado por la superficie \(S\). Cuando tenemos un campo escalar \(\phi\), el teorema establece que

(122)\[\int_{s}\phi ndS=\int_{v}\nabla\phi dV\]

Si utilizamos este resultado encontramos

(123)\[F=\int_{S}pndS=-\int_{v}\nabla\phi dV\]

Por otra parte, de la ecuación de la hidrostática sabemos que

(124)\[\nabla p=\rho g=-\rho gk\]

ya que \(\mathbf{g}=(0, 0, −g)\). Sustituyeno en la integral anterior obtenemos

(125)\[F=-\int_{V}\nabla pdV=\int_{V}\rho gkdV\]

es decir

(126)\[F_{e}=\rho Vgk\]

que es el resultado que encontramos antes para el cubo, a saber, que la fuerza de empuje es igual al peso del fluido desalojado y apunta en dirección vertical positiva.

Veamos cómo aplicamos este resultado en un ejemplo sencillo. Supongamos que queremos determinar el volumen desplazado \(V_{D}\) (o volumen sumergido) de un cuerpo sólido de densidad \(\rho _0\) que flota en un líquido de densidad \(\rho\). Si el volumen del cuerpo es \(V\) , aplicando el principio de Arquímedes tenemos que su peso debe igualarse con el empuje ejercido por el líquido (que es igual al peso del líquido desplazado), es decir,

(127)\[\rho_{0} V g = \rho V_D g\]

de modo que

(128)\[V_{D} = \frac{\rho_{0}}{\rho}V\]

donde vemos que el volumen desplazado es igual al cociente de las densidades multiplicado por el volumen del cuerpo. Por supuesto, midiendo el volumen desplazado de fluido, esta ecuación nos permite determinar la densidad del cuerpo. Si aplicamos este resultado a un cubo de hielo formado por agua dulce que flota en agua dulce contenida en un vaso ¿cuál será el volumen desplazado? Ya que al congelarse el agua aumenta su volumen, la densidad del hielo es ligeramente menor que la del agua líquida por lo que el volumen desplazado será un poco menor que el volumen del hielo. Las densidades del hielo y del agua dulce son \(916.8 \textrm{ kg/m}^{3}\) y \(1000 \textrm{ kg/m}^{3}\), respectivamente, por tanto poco más del \(8\%\) del volumen del hielo sobresale de la superficie, mientras que si el hielo flota en agua de mar cuya densidad es \(1027 \textrm{ kg/m}^{3}\), aproximadamente el volumen que sobresale es cercano al \(11\%\) del volumen del hielo. Por tanto, al derretirse el hielo el nivel del agua en el vaso subirá en un volumen equivalente a la parte del hielo que sobresale. Esto es lo que sucede con un iceberg en el océano donde la porción de hielo que sobresale de la superficie, al derretirse contribuye al aumento del nivel del océano. Analicemos ahora el caso de una esfera de acero de volumen \(V\) que se coloca en un recipiente que contiene mercurio. La densidad del acero es \(\rho_a=7850 \textrm{ kg/m}^{3}\), mientras que la del mercurio es \(\rho_{Hg}=13600 \textrm{ kg/m}^{3}\), por lo que la esfera flotará en el mercurio desplazando un volumen

(129)\[V_{DI}=\frac{\rho_{\alpha}}{\rho_{Hg}}V = 0.577 V\]

Dicho volumen lo podemos expresar como

(130)\[V_{DI}=x_{1}V\]

donde \(x_{1}=\rho_{a}/\rho _{Hg}=0.577\) es la fracción de volumen sumergida. Supongamos ahora que vertemos agua en el recipiente de manera que la esfera quede cubierta completamente, como se muestra en la Fig. 50. ¿Qué le pasará a la profundidad de inmersión de la esfera en el mercurio? Es decir, al verter el agua ¿la esfera emerge del mercurio o se sumerge más?

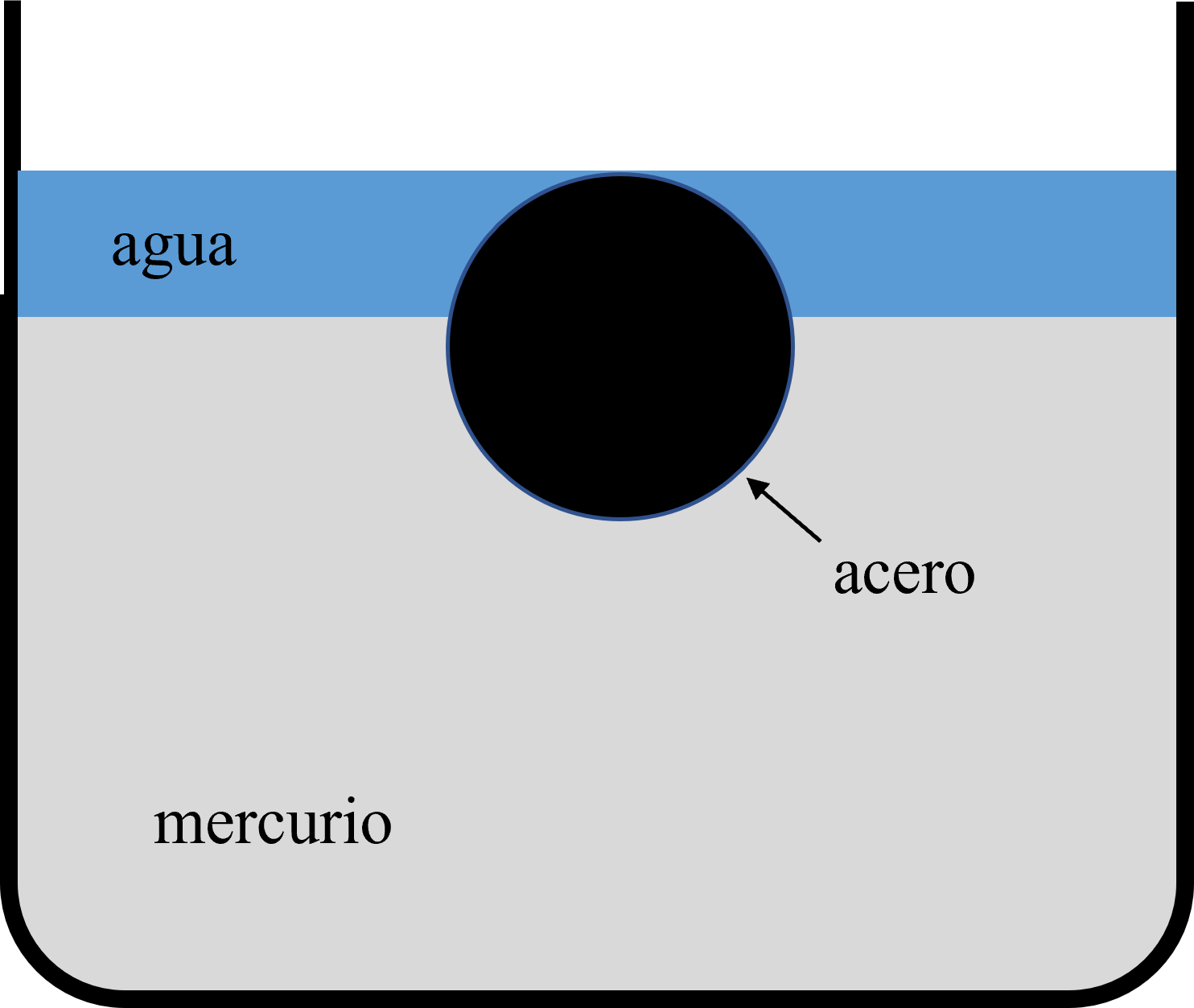
Fig. 50 Esfera de acero flotando en mercurio cubierta por una capa de agua.

En primera instancia, podría parecer que la capa de agua oprime a la esfera ocasionando que se hunda más. Sin embargo, al igual que el mercurio el agua también ejerce un empuje sobre la esfera de manera que el peso de la esfera se ve balanceado por el empuje que ejerce el mercurio más el que ejerce el agua. Si denotamos por \(\rho\) a la densidad del agua podemos establecer este balance en la forma

(131)\[\rho_{a}Vg=\rho V_{1}g+\rho_{Hg}V_{2}g\]

donde \(V_{1}\) y \(V_{2}\) son los volúmenes desplazados de agua y mercurio, respectivamente, los cuales satisfacen la relación \(V=V_{1}+V_{2}\). Sustituyendo \(V_{1}=V−V_{2}\) y eliminando \(g\), tenemos

(132)\[\rho_{a}V=\rho\left(V-V_{2}\right)+\rho_{Hg}V_{2}\]

de donde el voumen desplazado de mercurio es

(133)\[V_{2}=\frac{\rho_{a}-\rho}{\rho_{Hg}-\rho}V\]

o bien \(V_{2}=x_{2}V\) donde la fracción sumergida es

(134)\[x_{2}=\frac{\rho_{a}-\rho}{\rho_{Hg}-\rho}=0.543\]

es decir, \(x_{2}<x_{1}\) por lo que la profundidad de inmersión en el mercurio disminuye, o dicho en otras palabras, la esfera emerge un poco más al verter el agua.

Es interesante analizar un problema no hidrostático que involucra a la fuerza de flotación o empuje. Supongamos que sumergimos a la esfera de acero hasta el fondo del recipiente con mercurio y luego la liberamos, de manera similar a cuando sumergimos una pelota de plástico en una alberca. Como sabemos, la esfera será impulsada hacia arriba de manera acelerada por lo que podemos preguntarnos cuál es su aceleración inicial. Para responder esta pregunta debemos hacer uso de la segunda ley de Newton que nos dice que la masa del cuerpo, \(m\), por su aceleración, \(a\), es igual a la suma de todas las fuerzas que actúan sobre el cuerpo. En este caso, las fuerzas presentes son el peso del cuerpo, \(−F_{g}\), el empuje generado por el líquido desplazado, \(E\), y la fuerza viscosa, \(−F_{v}\), que manifiesta la fricción entre la esfera y el fluido. Notemos que todas ellas actúan en dirección vertical de modo que podemos escribir

(135)\[ma=-F_{g}+E-F_{v}\]

donde el signo menos indica que el peso y la fuerza viscosa actúan en dirección negativa, contraria al movimiento de la esfera. Ya que nos interesa calcular la aceleración en el instante en que se libera la esfera, para realizar un cálculo sencillo haremos una aproximación fuerte suponiendo que en un inicio la fuerza viscosa es despreciable. De esta forma, introduciendo la forma explícita del peso y el empuje en la ecuación (135), obtenemos

(136)\[\rho_{a}Va=-\rho_{a}Vg+\rho_{Hg}Vg\]

donde en el empuje hemos considerado que el volumen desplazado es igual al volumen total puesto que la esfera se encuentra totalmente sumergida. Despejando la aceleración, encontramos

(137)\[a=\frac{\rho_{Hg}-\rho_{a}}{\rho_{a}}g\]

donde vemos que la aceleración de la esfera es una fracción de la aceleración de la gravedad. Introduciendo los valores de las densidades del mercurio y el acero econtramos \(a=0.73g\), un valor que sobreestima la aceleración de la esfera puesto que se despreció la fuerza viscosa.

En realidad, la fuerza viscosa siempre está presente y si el recipiente de mercurio fuera suficientemente profundo, la esfera ascendería de manera acelerada solo durante una cierta distancia, alcanzando eventualmente una velocidad terminal (aceleración cero) cuando todas las fuerzas que actúan sobre la esfera se equilibran. Esto es similar a lo que ocurre con las gotas de lluvia cuya velocidad al alcanzar el piso es mucho menor que la que tendrían si cayeran en caída libre. Finalmente analicemos una situación menos común. Consideremos a un niño que sostiene un globo de helio dentro de un auto en reposo, como se muestra en la Fig. 51. Ya que el helio es mucho menos denso que el aire que rodea al globo, existe un empuje sobre el globo hacia arriba que es contrarrestado por el peso del globo y la tensión del hilo que lo sostiene. ¿Qué pasaría si repentinamente el auto adquiriera una aceleración horizontal constante hacia la derecha, \(a_c\)? Por experiencia, sabemos que debido a la inercia el cuerpo del niño se movería hacia atrás pero ¿qué le sucedería al globo? Por supuesto, por tener masa, la inercia también actuará sobre el globo impulsándolo hacia atrás, sin embargo, al moverse horizontalmente el globo desplaza al aire que lo rodea de manera que debe existir un empuje sobre el globo en esta dirección. Podemos plantear entonces la ecuación de movimiento para el globo en dirección horizontal, es decir,

(138)\[ma=E-ma_{c}\]

donde \(m\) es la masa del globo, \(a\) su aceleración, \(E\) el empuje horizontal, \(a_{c}\) la aceleración del auto y hemos despreciado la fuerza de fricción. El empuje es igual al peso del aire desplazado, es decir, \(E=\rho Vg\), donde \(\rho\) es la densidad del aire y \(V\) el volumen del globo. Entonces, si \(\rho_H\) es la densidad del helio, podemos escribir

(139)\[\rho_{H} V a= \rho V g- \rho_{H} V a_{c}\]

o bien

(140)\[a = \frac{\rho}{\rho_{H}}g - a_{c}\]

Ya que la densidad del aire es \(\rho = 1.29 \textrm{ kg/m}^{3}\) y la del helio es \(\rho _H = 0.178 \textrm{ kg/m}^{3}\), la aceleración del globo será \(a=(7.22)g−a_{c}\), que es una cantidad positiva siempre y cuando \(a_{c} < 7.22 g\), lo que ocurre para la aceleración común que puede adquirir un auto. Por tanto, el globo tendrá una aceleración positiva, inclinándose hacia adelante.

Fig. 51 a) Auto en reposo.

Fig. 52 b) Auto con aceleración constante \(a_c\) hacia la derecha.