Flujos viscosos unidireccionales#

El flujo de un fluido viscoso e incompresible sujeto a la fuerza gravitacional está descrito por las siguientes ecuaciones,

(273)#\[\nabla \cdot \mathbf{u}=0\]
(274)#\[\rho\left( \frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla) \mathbf{u} \right)= -\nabla p + \mu∇^{2} \mathbf{u} + \rho g\]

La ecuación de continuidad (273) y la ecuación de Navier-Stokes (274) forman un sistema de cuatro ecuaciones con cuatro incógnitas, a saber, las tres componentes de la velocidad, \(u\), \(v\), \(w\), y la presión, \(p\), las cuales son funciones de la posición y del tiempo. La solución de este sistema requiere satisfacer condiciones iniciales y de frontera específicas de cada problema y en general puede resultar muy complicada debido principalmente a que la ecuación (274) es no lineal. Hasta la fecha, no se conoce una solución general a estas ecuaciones, sin embargo, se han desarrollado una multitud de métodos numéricos para resolverlas y se han encontrado también diversas soluciones exactas que pueden obtenerse de forma analítica.

De manera expícita las ecuaciones (273) y (274) en coordenadas Cartesianas y en forma tridimensional, se expresan de la siguiente forma:

(275)#\[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,\]
(276)#\[ρ\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=−\frac{\partial p}{\partial x}+\mu\left(\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{\partial z^{2}}\right)\]
(277)#\[ρ\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=−\frac{\partial p}{\partial y}+\mu\left(\frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}+\frac{\partial ^{2}v}{\partial z^{2}}\right)\]
(278)#\[ρ\left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=−\frac{\partial p}{\partial z}+\mu\left(\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial y^{2}}+\frac{\partial ^{2}w}{\partial z^{2}}\right)−ρg\]

La solución de estas ecuaciones requiere especificar las condiciones de frontera que satisface el campo de velocidades. Sobre una superficie rígida, la condición de frontera que debe satisfacer cualquier flujo viscoso, independientemente de la magnitud de la viscosidad del fluido, es que las componentes normal y tangencial de la velocidad se igualen a las de la frontera misma. Esto quiere decir que si la frontera se encuentra en reposo, la velocidad debe anularse sobre ella. La condición sobre la componente tangencial de la velocidad se conoce como la condición de no deslizamiento.

En ciertos casos particulares se pueden realizar consideraciones que simplifican el problema a tal grado se puede resolver el sistema de ecuaciones (275)-(278) analíticamente de manera exacta. A continuación mostraremos algunos ejemplos de soluciones exactas de flujos unidireccionales que tienen la característica de que la aceleración del flujo se anula idénticamente.

Flujo de Couette#

Consideremos un fluido viscoso contenido entre dos paredes rígidas paralelas e infinitas, separadas por una distancia \(h\), una de las cuales está en reposo, mientras que la otra se mueve con una velocidad constante, \(U\), en dirección horizontal (\(x\)), como se muestra en la Fig. 66. El flujo se produce únicamente por el esfuerzo viscoso que ejerce la pared en movimiento sobre el fluido con el que está en contacto, ya que no existe un gradiente de presión en la dirección axial \(x\). Suponemos además que el flujo es laminar e independiente del tiempo. Se tiene entonces un flujo viscoso unidireccional estacionario que debe satisfacer condiciones de no deslizamiento en ambas paredes.

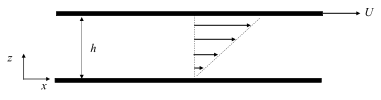
../../_images/Imagen_6.1.png

Fig. 66 Flujo de Covette producido por el movimiento de una pared plana#

Bajo las consideraciones anteriores, el campo de velocidades puede expresarse como

(279)#\[u=\left[ u\left( z \right), 0, 0 \right]\]

que podemos denominar como un flujo cortante paralelo. Si sustituimos este campo de velocidades en la ecuación de continuiddad (275) encontramos

(280)#\[\frac{\partial u}{\partial x}=0\]

donde observamos que se satisface idénticamente puesto que la componente \(u\) no depende de la coordenada \(x\), en la dirección de movimiento. Esta es una consecuencia de haber supuesto que las paredes que contienen al flujo son infinitas, lo que es equivalente a decir que los efectos de borde, que se presentarían en los extremos de las paredes, son inexistentes. Los flujos que son independientes de la coordenada en la dirección del movimiento se denominan flujos completamente desarrollados. Sustituyendo le campo de velocidades en el lado izquierdo de la ecuación (276), encontramos

(281)#\[\rho\left( \cancel{\frac{\partial u}{\partial t}}+ u \cancel{\frac{\partial u}{\partial x}}+\cancel{v} \cancel{\frac{\partial u}{\partial y}}+\cancel{w} \frac{\partial u}{\partial z} \right) = 0\]

y ya que \(\partial p/\partial x = 0\), la ecuación (276) se reduce a

(282)#\[\frac{\partial^{2}u}{\partial z^{2}}=0\]

cuya solución es

(283)#\[u(z)=Az+B\]

donde \(A\) y \(B\) son las constantes de integración que deben determinarse imponiendo las condiciones a la frontera sobre las paredes, es decir, las condiciones de no deslizamiento. Dado que el origen del sistema coordenado se ha colocado en la pared inferior (ver Fig. 66), tenemos

(284)#\[u(0)=0\]
(285)#\[u(h)=U\]

Finalmente, la solución es

(286)#\[u(z)=U\frac{z}{h}\]

es decir, se trata de un perfil de velocidades lineal. Por otra parte, de la ecuación (278) se obtiene

(287)#\[0=−\frac{\partial p}{\partial z}−ρg\]

de donde

(288)#\[p(z)=p_{0}-\rho gz\]

lo que nos indica que la presión varía hidrostáticamente en dirección \(z\) sin afectar el movimiento, donde \(p_0\) es una constante a determinar. Del perfil de velocidades (286), observamos que la velocidad máxima se da en \(z = h\) y es precisamente la velocidad de la pared \(U\). Por otro lado, podemos calcular el flujo volumétrico a por unidad de profundidad, través de cualquier sección transversal del ducto, es decir,

(289)#\[Q=\int_{0}^{h} u(z) dz=U\frac{z^{2}}{2h}|_{0}^{h}=\frac{Uh}{2}\]

de modo que la velocidad media es

(290)#\[u_{m}=\frac{Q}{A}=\frac{U}{2}\]

donde \(A = h\) es el área de la sección transversal que por tratarse de un flujo plano es simplemente una línea. Por último, podemos calcular el esfuerzo cortante dado por

(291)#\[\sigma_{zx}=\mu\frac{\partial u}{\partial z}=\mu\frac{U}{h}\]

es cual es constante en toda la región del flujo. Ahora definimos el coeficiente de fricción en la forma

(292)#\[C_{f}=\frac{\sigma_{zx}|_{pared}}{\frac{1}{2}\rho u_{m}^{2}}\]

que es un parámetro adimensional que cuantifica el esfuerzo viscoso en la pared. Sustituyendo el valor de \(\sigma _{zx}\) y \(u_m\), encontramos

(293)#\[C_{f}=\frac{8\mu}{\rho Uh}\]

En términos del número de Reynolds

(294)#\[Re=\frac{\rho Uh}{\mu}\]

donde \(U\) y \(h\) son las escalas de velocidad y longitud características, podemos expresar al coeficiente de fricción como

(295)#\[C_{f}=\frac{8}{Re}\]

Este resultado es válido únicamente para flujos laminares y nos indica que la fricción en la pared disminuye conforme aumenta el número de Reynolds.

Flujo de Hagen-Poiseuille#

Ahora analizaremos un flujo viscoso que tiene lugar entre dos paredes paralelas infinitas que se encuentran en reposo, el cual es impulsado por un gradiente de presión constante en dirección \(x\), como se muestra en la Fig. 67. Al igual que en el caso anterior, suponemos que el flujo es laminar, estacionario y completamente desarrollado, de modo que el campo de velocidades es de la forma

(296)#\[\mathbf{u} = \left[ u(z),0,0 \right]\]

Por tanto, la ecuación de continuidad (275) se satisface idénticamente y las componentes de la ecuación de Navier-Stokes en direcciones \(x\) y \(z\), (ecuaciones (276) y (278)), se reducen a

(297)#\[0=-\frac{\partial p}{\partial x}+\mu\frac{\partial ^{2}u}{\partial z^{2}}\]
(298)#\[0=-\frac{\partial p}{\partial z}-\rho g\]
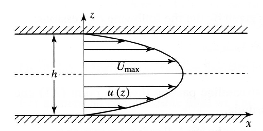
../../_images/Imagen_6.2.png

Fig. 67 Flujo de Hagen-Poiseuille producido por un gradiente de presión axial.#

La ecuación (298) es la ecuación de la hidrostática, y al integrarla respecto a la coordenada \(z\) obtenemos

(299)#\[p=-\rho gz+C(x),\]

donde \(C(x)\) es a lo más una función de \(x\). Si derivamos esta ecuación respecto a \(x\), encontramos

(300)#\[\frac{\partial p}{\partial x}=C^{'}(x),\]

donde \(C'(x) =\) constante, ya que hemos supesto que el gradiente de presión axial es constante. Si denominamos \(\partial p/\partial x = −G\) e intergramos, la presión queda

(301)#\[p(x,z)=-\rho gz-Gx+p_{0},\]

donde \(p_0\) es una constante de integración. Debe notarse que \(− \partial p/ \partial x = G > 0\) por lo que el flujo se desplaza de izquierda a derecha.

Por otro lado, la ecuación (297) se puede expresar en la forma

(302)#\[\frac{\partial ^{2}u}{\partial z^{2}}=-\frac{G}\mu\]

y al integrar obtenemos

(303)#\[u\left(z\right)=-\frac{G}{µ}\frac{z^{2}}{2}+Az+B\]

Aplicando las condiciones de no deslizamiento en las paredes

(304)#\[u(0)=u(h)=0\]

obtenemos un perfil parabólico, es decir,

(305)#\[u(z)=\frac{G}{2\mu}z\left(h-z\right)=\frac{Gh^{2}}{2\mu}\left(1-\frac{z}{h}\right)\frac{z}{h}\]

La velocidad máxima se encuentra en el punto medio entre las paredes, \(z = h/2\), y su valor es

(306)#\[U_{max}=\frac{Gh^{2}}{8\mu}\]

A su vez, el gasto volumétrico por unidad de profundidad está dado por

(307)#\[Q=\frac{Gh^{2}}{2\mu}\int_{0}^{h}\left(1-\frac{z}{h}\right)\frac{z}{h}dz=\frac{Gh^{3}}{12\mu}\]

mientras que la velocidad media es

(308)#\[u_{m}=\frac{Q}{h}=\frac{Gh^{2}}{12\mu}\]

El esfuerzo cortante en cualquier punto del fluido es

(309)#\[\sigma_{zx}={\mu}\frac{\partial u}{\partial z} = \frac{Gh^{2}}{2}\left(\frac{1}{h}-\frac{2z}{h^{2}}\right)\]

por lo que en la pared inferior tenemos

(310)#\[\sigma_{yx}|_{z=0}=\frac{Gh}{2}\]

y en la pared superior se obtiene

(311)#\[\sigma_{zx}|_{z=0}=-\mu \left. \frac{\partial u}{\partial z} \right|_{z=0}=\frac{Gh}{2}\]

donde el signo menos se debe a que la normal a la pared apunta en dirección negativa, hacia donde se encuentra el fluido. El coeficiente de fricción en cualquiera de las paredes es

(312)#\[C_{f}=\frac{\sigma_{zx}|_{z=0,h}}{\rho u_{m}^{2}/2}=\frac{Gh}{\rho u_{m}^{2}}\]

el cual puede reescribirse solo en términos de la velocidad media usando la ecuación (308), es decir,

(313)#\[C_{f}=\frac{12\mu}{\rho u_{m}h}=\frac{12}{Re}\]

donde el número de Reynolds está dado por \(Re = \rho u_m h/\mu \). Si consideramos un tramo del ducto de longitud \(L\), podemos calcular la fuerza viscosa total (por unidad de profundidad) en dirección \(x\) ejercida sobre las paredes por el fluido, esto es

(314)#\[F_{x}= \left[ \sigma_{zx}(0) + \sigma_{zx}(h) \right] L = G h L\]

Ya que el gradiente de presión se puede aproximar como

(315)#\[G=-\frac{\partial p}{\partial x} \approx \frac{\Delta p}{L}\]

donde \( \Delta p\) es la diferencia de presiones entre los extremos de la sección de longitud \(L\), encontramos

(316)#\[F_{x}=\Delta p h\]

Notemos que \(\Delta p h\) es igual a la diferencia de las fuerzas de presión que actúan en los extremos de la sección del ducto. Este resultado nos muestra que la fuerza de presión neta ejercida sobre el fluido se equilibra con el esfuerzo viscoso cortante integrado sobre las paredes del ducto.

Superposición de los flujos de Couette y Hagen-Poiseuille#

Consideremos ahora el caso de un flujo entre dos paredes paralelas infinitas producido por la acción simultánea de una pared en movimiento y un gradiente de presión axial. Podemos plantear el problema de manera similar al caso anterior por lo que la presión está dada por la ecuación (301). Asimismo, la ecuación de movimiento es la misma que para el flujo de Hagen-Poiseuille

(317)#\[\frac{\partial ^{2}u}{\partial z^{2}}=-\frac{G}{\mu}\]

excepto que ahora las condiciones de frontera corresponden a las del flujo de Couette, es decir

(318)#\[u(0)=0,\]
(319)#\[u(h)=U.\]

La solución de este problema de valores de frontera nos permite encontrar el perfil de velocidades buscado. Sin embargo, también podemos obtener la solución utilizando el principio de superposición que aplica para las ecuaciones diferenciales lineales. Es decir, el problema planteado tiene como solución a la suma del flujo de Couette (286) y el flujo de Hagen-Poiseuille (305), esto es

(320)#\[u(z)=U\frac{z}{h}+\frac{Gh^{2}}{2\mu}\left(1-\frac{z}{h}\right)\frac{z}{h}\]

Notemos que el gradiente de presión puede aplicarse de izquierda a derecha \((G > 0)\) o de derecha a izquierda \((G < 0)\), por lo que puede ir a favor o en contra del movimiento de la pared.

Película descendente en una pared vertical#

La Fig. 68 ilustra una situación en donde una delgada película de un líquido viscoso desciende sobre una pared vertical debido a la acción de la gravedad. Al igual que en los casos considerados anteriormente, suponemos que el flujo es estacionario y que la pared vertical es infinita de manera que se establece un flujo completamente desarrollado. Suponemos también que no existe un gradiente de presión que actúe en la dirección del movimiento, siendo la gravedad la única causa que provoca el desplazamiento del fluido. Por consistencia con el análisis de los flujos previos, colocamos el sistema coordenado sobre la pared vertical con el eje \(x\) apuntando hacia abajo y el eje \(z\) transversal a la pared. De esta forma, la gravedad apunta en dirección \(x\) positiva.

A diferencia de los casos anteriores en donde el flujo está confinado entre paredes rígidas, en este flujo solo una de las fronteras es rígida, mientras que la otra es lo que llamamos una superficie libre, es decir, la interfaz entre el líquido viscoso y el aire de la atmósfera, lo que introduce un elemento nuevo en el flujo.

Dadas las suposiciones hechas previamente, el campo de velocidades es de la forma

(321)#\[u= \left[ u(z),0,0 \right]\]

donde las fronteras del flujo están en \(z = 0\) y en \(z = h\), siendo \(h\) el grosor de la película. Con esta suposición, la ecuación de continuidad se satisface idénticamente.

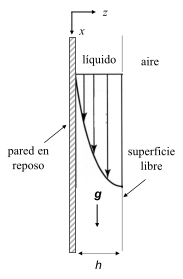
../../_images/Imagen_6.3.png

Fig. 68 Flujo de Couette producido por el movimiento de una pared plana#

Analicemos primero que pasa con la presión. La componente \(z\) de la ecuación de Navier-Stokes se reduce a

(322)#\[\frac{\partial p}{\partial z}=0\]

lo que nos indica que la presión no es una función de la coordenada \(z\), y a lo más será una función de \(x\), es decir, \(p = p(x)\). Sin embargo, la presión debeser continua a través de la interfaz líquido-aire, de modo que debemos tener

(323)#\[p(x)=p_{atm} \, \textrm{, en } z=h\]

de donde deducimos que p debe ser constante, de modo que \(\partial p/\partial x = 0\). Por tanto, la ecuación de movimiento en dirección \(x\) toma la forma

(324)#\[0=\mu\frac{\partial ^{2}u}{\partial z^{2}}+\rho g\]

y al integrarla obtenemos

(325)#\[u(z)=-\frac{\rho g}{\mu}\frac{z^{2}}{2} + Az + B\]

donde las constantes de integración A y B se determinan aplicando las condiciones de frontera. Sobre la pared vertical la condición es de no deslizamiento, es decir,

(326)#\[u(0)=0\]

Por otra parte, sobre la superficie libre imponemos la condición de ausencia de esfuerzos cortantes en la interfaz líquido-aire, esto es

(327)#\[\sigma_{zx}|_{z=h} = {\mu} \left. \frac{\partial u}{\partial z} \right|_{z=h}=0\]

lo que se reduce a

(328)#\[\frac{\partial u}{\partial z}=0 \, , \textrm{ en } z=h\]

Esta es la condición más sencilla que podemos imponer sobre una superficie libre y asume que el aire en contacto con el líquido está en reposo de modo que no perturba la interfaz, por lo que esta permanece plana. Aplicando las condiciones de frontera obtenemos

(329)#\[u(z)=\frac{\rho g}{2{\mu}}z(2h-z)\]

donde observamos que se trata de un flujo parabólico cuya velocidad máxima se da precisamente en la interfaz líquido-aire, es decir, en \(z = h\):

(330)#\[U_{max}=\frac{\rho gh^{2}}{2{\mu}}\]

Por su parte, el flujo volumétrico por unidad de profundidad es

(331)#\[Q = \int_{0}^{h} u\left(z\right)dz = \frac{\rho g}{2{\mu}} \int_{0}^{h}z(2h-z)dz=\frac{\rho gh^{3}}{3{\mu}}\]

de donde la velocidad media es

(332)#\[u_{m}=\frac{Q}{h}=\frac{\rho gh^{2}}{3{\mu}}\]

A su vez, el esfuerzo cortante en la pared es

(333)#\[\sigma_{zx}|_{z=0}={\mu} \left. \frac{\partial u}{\partial z} \right|_{z=0} = \rho g h\]

y por tanto, el coeficiente de fricción queda

(334)#\[C_{f}=\frac{\sigma|_{z=0}}{\rho u_{m}^{2}/2}=\frac{\rho gh}{\rho u_{m}^{2}/2}\]

Para poder expresarlo en términos del número de Reynolds, utilizamos la ecuación (332), de donde

(335)#\[\rho gh=\frac{3{\mu}u_{m}}{h}\]

por lo que finalmente podemos escribir

(336)#\[C_f=\frac{6\mu}{ρu_{m}h}=\frac{6}{Re}\]

Al igual que en los casos anteriores vemos que la fricción disminuye al aumentar el número de Reynolds.

Flujo de Poiseuille#

Ahora analizaremos uno de los flujos más comunes que tienen lugar en múltiples aplicaciones e incluso en sistemas biológicos, a saber, el flujo en un tubo recto de sección transversal circular constante producido por una diferencia de presión entre sus extremos, conocido como flujo de Poiseuille. Supondemos, de manera similar a los casos anteriores, que el flujo es independiente del tiempo y que tiene lugar en un tubo infinito, de manera que los efectos de borde son inexistentes por lo que puede considerarse completamente desarrollado. Dada la geometría del ducto, es conveniente utilizar coordenadas cilíndricas \((r, θ, z)\) para su descripción, haciendo coincidir el eje \(z\) con el eje de simetría del cilindro, como se muestra en la Fig. 69.

../../_images/Imagen_6.4.png

Fig. 69 Flujo de Covette producido por el movimiento de una pared plana#

Con las suposiciones anteriores, el campo de velocidades es de la forma

(337)#\[\mathbf{u} = \left[ 0, 0, u_{z}(r) \right]\]

de modo que la ecuación de continuidad se satisface idénticamente:

(338)#\[\frac{\partial u_{z}}{\partial z} = 0\]

Por su parte, la componente \(z\) de la ecuación de Navier-Stokes resulta

(339)#\[\rho \left( \mathbf{u} \cdot \nabla \right) u_{z}=-\frac{\partial p}{\partial z} + \mu \nabla^{2} u_{z}-\rho g \sin \alpha\]

donde \(\alpha\) es el ángulo que forma el eje del tubo con la horizontal. Para el ducto mostrado en la Fig. 69, dicho ángulo es \(\alpha = 0\) por lo que la gravedad no tiene un efecto sobre el flujo. A su vez, el término de aceleración convectiva es nulo

(340)#\[\left( \mathbf{u} \cdot \nabla \right) u_{z} = u_{z} \frac{\partial u_{z}}{\partial z} = 0\]

por tratarse de un flujo completamente desarrollado. La ecuación de movimiento se reduce entonces a la forma

(341)#\[\nabla^{2}u_{z}=\frac{1}{\mu}\frac{\partial p}{\partial z}\]

donde el gradiente de presión axial es constante. Si hacemos \(G = −\partial p/\partial z > 0\), y expresamos el lapaciano en coordenadas cilíndricas, tenemos la ecuación

(342)#\[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{z}}{\partial z}\right)=-\frac{G}{\mu}\]

que puede integrarse directamente para encontrar

(343)#\[u_{z}(r)=-\frac{G}{\mu}\frac{r^{2}}{4} + A\ln r + B\]

Podemos determinar las constantes de integración \(A\) y \(B\) aplicando la condición de no deslizamiento sobre las paredes del ducto e imponiendo que la velocidad en el centro del flujo, aunque desconocida, sea finita. Es decir,

(344)#\[u_{z}=0 \, , \textrm{ en } r=0\]
(345)#\[u_{z} = \textrm{ finita , en } r = R\]

La condición (345) implica que \(A = 0\), ya que de otra manera habría una discontinuidad en el origen. Esta condición es equivalente a pedir que el flujo sea simétrico respecto al eje del cilindro, lo que lleva a imponer que \(du_z/dr = 0\) en \(r = 0\).

Aplicando las condiciones de frontera, el perfil de velocidades queda

(346)#\[u_{z}(r)=\frac{GR^{2}}{4\mu}\left[1-\left(\frac{r}{R}\right)^{2}\right]\]

que es un flujo parabólico cuya velocidad máxima se alcanza en el centro del ducto:

(347)#\[U_{max}=\frac{GR^{2}}{4\mu} \, , \textrm{ en } r=0\]

Por su parte, el gasto volumétrico a través de cualquier sección transversal del ducto es

(348)#\[Q=\int_{0}^{2\pi}\int_{0}^{R}u_{z}(r)r\partial r\partial \theta\]
(349)#\[=\frac{G\pi R^{2}}{2\mu}\int_{0}^{R}\left[1-\left(\frac{r}{R}\right)^{2}\right]rdr\]
(350)#\[=\frac{G\pi R^{4}}{8\mu}\]

por lo que, al dividir entre el área de la sección transversal, encontramos la velocidad media

(351)#\[u_{m}=\frac{GR^{2}}{8{\mu}0}\]

Finalmente, el esfuerzo cortante en las paredes del ducto es

(352)#\[\sigma_{rz}|_{r=R}=-{\mu} \left. \frac{\partial u_{z}}{\partial r} \right|_{r=R}\]

donde el signo menos indica que la normal en la pared apunta en dirección negativa. Explícitamente encontramos

(353)#\[\sigma_{rz}|_{r=R} = {\mu}\frac{GR^{2}}{4\mu} \left. \frac{2r}{R^{2}} \right|_{r=R}=\frac{GR}{2}\]

Podemos entonces calcular el coeficiente de fricción como

(354)#\[C_{f}=\frac{\sigma_{rz}|_{r=R}}{\rho u_{m}^{2}/2}=\frac{GR/2}{\rho u_{m}^{2}/2}\]

y utilizando la ecuación (351) para expresar el gradiente de presión en términos de la velocidad media, encontramos

(355)#\[C_f = \frac{16\mu}{\rho u_{m}(2R)} = \frac{16}{Re}\]

donde el número de Reynolds se ha definido utilizando el diámetro del tubo, \(D = 2R\), como longitud caracterísitca. La ecuación (355) es de gran utilidad para el cálculo del flujo en tuberías. Debemos enfatizar que la solución para el flujo de Poiseuille y consecuentemente el resultado (355), se ha obtenido bajo la suposición de que el flujo está en régimen laminar, lo cual sucede en este caso particular, aproximadamente cuando el número de Reynolds es menor a 2000.

Ley de Poiseuille#

Para diversas aplicaciones es conveniente conocer la relación entre el gasto volumétrico a través de un tubo y la diferencia de presión que existe entre sus extremos. Dicha relación se conoce como la ley de Poiseuille y puede obtenerse de manera simple a partir de los resultados que encontramos previamente.

La ecuación (350) nos da la relación entre el gasto volumétrico y el gradiente de presión axial

(356)#\[Q=\frac{G\pi R^{4}}{8\mu}\]

Aunque hemos supuesto que el tubo es de longitud infinita, podemos aproximar el gradiente de presión en una sección del tubo de longitud \(L\), en la forma

(357)#\[G=-\frac{\partial p}{\partial z}\approx\frac{\Delta p}{L}\]

donde hemos introducido la diferencia de presión entre los extremos de la sección del tubo, \(\Delta p = p_{alta} − p_{baja}\). De este modo, el gasto volumétrico puede expresarse como

(358)#\[Q=\frac{\pi R^{4}}{8\mu}\frac{\Delta p}{L}\]

o bien en términos del diámetro

(359)#\[Q=\frac{\pi D^{4}}{128\mu}\frac{\Delta p}{L}\]

La ecuación (359) se conoce como la ley de Poiseuille y a la cantidad

(360)#\[R_{h}=\frac{128{\mu}L}{\pi D^{4}}\]

se le denomina la resistencia hidráulica, en analogía con la resistencia eléctrica, \(R_e\), que aparece en la ley de Ohm de los circuitos eléctricos:

(361)#\[I=\frac{\Delta V}{R_{e}}\]

donde \(I\) es la intensidad de la corriente eléctrica y \(\Delta V\) el voltaje aplicado. Notemos que la resistencia hidráulica es directamente proporcional a la viscosidad del fluido, \(\mu\), y a la longitud del tubo, \(L\), e inversamente proporcional al diámetro, \(D\), del mismo.

El flujo de Poiseuille (346) se encontró suponiendo que el tubo está en posición horizontal, sin embargo, si el eje del tubo forma un ángulo \(\alpha\) distinto de cero con la horizontal, podemos generalizar dicha solución en la forma

(362)#\[u_{z}(r)=\frac{(G-\rho g \sin \alpha)R^{2}}{4{\mu}}\left[ 1-\left(\frac{r}{R} \right)^{2} \right]\]

De igual manera, para un tubo con un ángulo de inclinación arbitrario respecto a la horizontal (ver Fig. 70), la ley de Poiseuille toma la forma

(363)#\[Q=\frac{\pi D^{4}(\Delta p-\rho g L \sin \alpha)}{128{\mu}L}\]

donde observamos que para una \(\Delta p\) dada, el gasto será mayor o menor de acuerdo al valor del ángulo \(\alpha\). Así, cuando \(\alpha = \pi / 2\), tenemos

(364)#\[Q=\frac{\pi D^{2}(\Delta p-\rho gL)}{128{\mu}L}\]
../../_images/Imagen_6.5.png

Fig. 70 Flujo de Poiseuille en un tubo cuyo eje forma un ángulo \(\alpha\) con la horizontal#

donde la gravedad se opone al flujo de modo que la diferencia de presión debe vencer no solo a la fricción dentro del tubo sino al peso de la columna de fluido. Por otra parte, si \(\alpha = 3 \pi/2\),

(365)#\[Q=\frac{\pi D^{4}(\Delta p+\rho gL)}{128{\mu}L}\]

y en este caso la gravedad contribuye junto con la diferencia de presión a impulsar al flujo.